توزیع سرعت ماکسول
توزیع سرعت ماکسول (Maxwell Speed Distribution): مفاهیم، فرمولها و مثالها
توزیع سرعت ماکسول یکی از مفاهیم کلیدی در فیزیک و شیمی حرارتی است که برای توصیف چگونگی توزیع سرعتهای مولکولهای یک گاز ایدهآل استفاده میشود. این توزیع نشان میدهد که چگونه مولکولهای یک گاز با دما و جرم مولی مشخص، سرعتهای متفاوتی دارند. در این مقاله به تعریف دقیقتر این مفهوم، فرمولهای مرتبط، اصول پایه و مثالهای کاربردی خواهیم پرداخت تا به صورت ساده و قابل فهم برای همگان ارائه شود. همچنین سؤالاتی مطرح خواهیم کرد که شما را به تفکر بیشتر در این زمینه دعوت میکند.
مفهوم توزیع سرعت ماکسول
توزیع سرعت ماکسول که به نام جیمز کلارک ماکسول (فیزیکدان مشهور اسکاتلندی) نامگذاری شده است، نشان میدهد که در یک گاز ایدهآل، مولکولها به طور یکسان سرعتهای مختلفی ندارند، بلکه برخی از آنها سرعت بالاتری دارند و برخی دیگر سرعتهای پایینتری. این توزیع به صورت تابعی از سرعتها تعریف میشود که میتوان آن را به صورت زیر بیان کرد:
![]()
که در آن:
![]() : تابع توزیع سرعت است که نشان میدهد چه نسبتی از مولکولها دارای سرعتی بین
: تابع توزیع سرعت است که نشان میدهد چه نسبتی از مولکولها دارای سرعتی بین ![]() و
و ![]() هستند.
هستند.
![]() : جرم مولی گاز (به کیلوگرم بر مول).
: جرم مولی گاز (به کیلوگرم بر مول).
![]() : ثابت گازها (8.314 J/mol.K).
: ثابت گازها (8.314 J/mol.K).
![]() : دمای مطلق (به کلوین).
: دمای مطلق (به کلوین).
![]() : سرعت مولکول (به متر بر ثانیه).
: سرعت مولکول (به متر بر ثانیه).
نکته کلیدی: توزیع سرعتها تحت تأثیر دما و جرم مولی است. با افزایش دما، توزیع به سمت سرعتهای بالاتر منتقل میشود و مولکولهای سبکتر تمایل به داشتن سرعتهای بیشتری دارند.
سه سرعت کلیدی در توزیع سرعت ماکسول
برای درک بهتر توزیع سرعت ماکسول، سه نوع سرعت کلیدی وجود دارد که هر یک از آنها نمایانگر جنبهای از توزیع مولکولهاست:
1. سرعت متوسط (Average Speed: 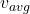 )
)
سرعت متوسط میانگین تمام سرعتهای مولکولهای گاز را نشان میدهد و از طریق رابطه زیر محاسبه میشود:
![]()
این رابطه نشان میدهد که سرعت متوسط با دما نسبت مستقیم و با جرم مولی گاز نسبت عکس دارد. به عبارت دیگر، با افزایش دما، مولکولها به طور میانگین سریعتر حرکت میکنند، اما مولکولهای سنگینتر سرعت کمتری دارند.
2. سرعت محتملترین (Most Probable Speed: 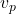 )
)
سرعت محتملترین، سرعتی است که بیشترین تعداد مولکولها در یک گاز ایدهآل دارند. به عبارت دیگر، این سرعت بهعنوان اوج تابع توزیع سرعت ماکسول شناخته میشود. رابطهی محاسباتی آن به صورت زیر است:
![]()
3. سرعت موثر یا RMS (Root Mean Square Speed: 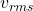 )
)
سرعت مؤثر (یا RMS) اندازهای است که بر اساس میانگین مربع سرعتها محاسبه میشود و به دلیل توان دوم سرعتها، معمولاً بزرگتر از سرعت متوسط است. فرمول محاسبه سرعت RMS به شرح زیر است:
![]()
تفاوتها بین این سه سرعت
این سه سرعت به ما دیدگاههای مختلفی از توزیع سرعتها میدهند:
- سرعت محتملترین نشان میدهد کدام سرعت بیشترین احتمال وقوع را دارد.
- سرعت متوسط میانگین تمام سرعتهای مولکولهاست.
- سرعت RMS بیشتر تحت تأثیر مولکولهایی با سرعتهای بالا قرار میگیرد.
سوال برای تفکر:
چرا سرعت RMS همواره از سرعت متوسط و سرعت محتملترین بیشتر است؟ چه عواملی باعث میشوند که این تفاوتها وجود داشته باشد؟
مثال: محاسبه سرعتها برای گاز اکسیژن
فرض کنید گاز اکسیژن (![]() ) در دمای 300 کلوین قرار دارد. جرم مولی اکسیژن
) در دمای 300 کلوین قرار دارد. جرم مولی اکسیژن ![]() است. برای محاسبه سرعتها به جرم مولی بر حسب کیلوگرم بر مول نیاز داریم:
است. برای محاسبه سرعتها به جرم مولی بر حسب کیلوگرم بر مول نیاز داریم:
![]()
حال با استفاده از فرمولهای بالا، سرعتهای مختلف را برای گاز اکسیژن محاسبه میکنیم:
محاسبه سرعت متوسط:
![]()
محاسبه سرعت محتملترین:
![]()
محاسبه سرعت RMS:
![]()
این نتایج نشان میدهند که سرعت RMS بزرگتر از سرعت متوسط است و سرعت محتملترین کمتر از هر دو است. همچنین میبینیم که سرعتها به شدت به جرم مولی و دما وابسته هستند.
سوال برای تفکر:
اگر دمای گاز دو برابر شود، هر یک از این سرعتها چگونه تغییر میکنند؟ آیا افزایش دما به همان نسبت بر سرعتها تأثیر میگذارد؟
تأثیر دما و جرم مولی بر توزیع سرعت ماکسول
یکی از جنبههای جذاب توزیع ماکسول این است که چگونگی توزیع سرعتها به دو عامل کلیدی وابسته است: دما و جرم مولی.
تأثیر دما
وقتی دما افزایش مییابد، مولکولهای گاز انرژی جنبشی بیشتری دریافت میکنند. در نتیجه، مولکولها سریعتر حرکت میکنند و توزیع سرعت به سمت سرعتهای بالاتر منتقل میشود. به همین دلیل است که گازها در دماهای بالاتر تمایل به انتشار سریعتر دارند.
تأثیر جرم مولی
جرم مولی یک گاز نیز نقش مهمی در تعیین سرعتهای مولکولهای آن دارد. مولکولهای سنگینتر (مانند مولکولهای گاز اکسیژن) به دلیل جرم بیشتر، سرعت کمتری نسبت به مولکولهای سبکتر (مانند مولکولهای هیدروژن) دارند.
مثال: مقایسه توزیع سرعتهای هیدروژن و اکسیژن
در دمای ثابت، مولکولهای هیدروژن ![]() به دلیل جرم مولی بسیار کمتر، سرعتهای بسیار بیشتری نسبت به مولکولهای اکسیژن دارند. این تفاوت در سرعتها یکی از دلایلی است که هیدروژن به عنوان یک گاز سبکتر، سریعتر از اکسیژن در فضا پخش میشود.
به دلیل جرم مولی بسیار کمتر، سرعتهای بسیار بیشتری نسبت به مولکولهای اکسیژن دارند. این تفاوت در سرعتها یکی از دلایلی است که هیدروژن به عنوان یک گاز سبکتر، سریعتر از اکسیژن در فضا پخش میشود.
سوال برای تفکر:
چرا مولکولهای سبکتر با سرعت بیشتری حرکت میکنند؟ چگونه میتوان این موضوع را از نظر فیزیکی توضیح داد؟
کاربردهای توزیع سرعت ماکسول
توزیع سرعت ماکسول تنها یک مفهوم نظری نیست، بلکه در بسیاری از زمینههای علمی و صنعتی کاربرد دارد:
1. فیزیک حرارتی
در فیزیک حرارتی، توزیع ماکسول به ما کمک میکند تا رفتار گازها در دماهای مختلف را تحلیل کنیم. این توزیع به ویژه در بررسی واکنشهای شیمیایی که به سرعت مولکولها بستگی دارد، اهمیت دارد.
2. موتورهای جت و هوافضا
در طراحی موتورهای جت و سیستمهای پیشرانه، دانش توزیع سرعت مولکولهای گازها به مهندسان کمک میکند تا کارایی موتورها را بهینهسازی کنند.
3. شیمی محیط زیست
در مطالعه انتشار آلایندهها در جو، توزیع سرعت ماکسول به شیمیدانان کمک میکند تا رفتار مولکولهای مختلف را در محیط پیشبینی کنند.
4. فناوری نانو
در مقیاس نانو، رفتار مولکولها به سرعتهای آنها بستگی دارد. به همین دلیل، در طراحی نانوماشینها و نانومواد، توزیع سرعت ماکسول یک ابزار مفید است.
