موقعیت زاویه ای
موقعیت زاویهای (Angular Position) در فیزیک: توضیحی جامع و کاربردی
در فیزیک، موقعیت زاویهای یا Angular Position یکی از مفاهیم اساسی در بحث حرکت دورانی اجسام است. این مفهوم به ما کمک میکند تا چرخش یک جسم صلب را حول یک محور ثابت توصیف کنیم. در این مقاله، به زبان ساده و با ارائه مثالهای متنوع، اصول و مفاهیم موقعیت زاویهای را بررسی میکنیم و فرمولها و کاربردهای آن را توضیح میدهیم.
تعریف موقعیت زاویهای: نقطه شروع در حرکت دورانی
وقتی یک جسم صلب حول یک محور ثابت میچرخد، برای توصیف موقعیت آن در هر لحظه نیاز به یک موقعیت زاویهای (Angular Position) داریم. برای این کار، ابتدا یک خط مرجع را در نظر میگیریم که در داخل جسم ثابت شده و عمود بر محور چرخش است. موقعیت زاویهای این خط مرجع را نسبت به یک جهت ثابت در فضا اندازهگیری میکنیم. زاویهی بهدستآمده نشاندهنده موقعیت زاویهای جسم است.
برای اندازهگیری این زاویه از واحد رادیان استفاده میکنیم. هرگاه زاویه به رادیان اندازهگیری شود، فرمول موقعیت زاویهای بهصورت زیر است:
![]()
که در آن:
![]() زاویه به رادیان است.
زاویه به رادیان است.
![]() طول قوس مسیر دایرهای طیشده توسط جسم است.
طول قوس مسیر دایرهای طیشده توسط جسم است.
![]() شعاع دایرهای است که جسم روی آن حرکت میکند.
شعاع دایرهای است که جسم روی آن حرکت میکند.
واحد رادیان چیست؟
رادیان یکی از واحدهای استاندارد برای اندازهگیری زاویه است. در یک دایره کامل، وقتی قوس مسیر با شعاع دایره برابر باشد، زاویه متناظر با آن یک رادیان است. از آنجا که محیط یک دایره کامل ![]() است، زاویه یک دور کامل در واحد رادیان برابر با
است، زاویه یک دور کامل در واحد رادیان برابر با ![]() رادیان خواهد بود. این معادل ۳۶۰ درجه است:
رادیان خواهد بود. این معادل ۳۶۰ درجه است:
![]()
بنابراین برای تبدیل زاویه از درجه به رادیان و بالعکس، از روابط زیر استفاده میکنیم:
![]()
![]()
فرمولهای مهم و اصول پایه
برای محاسبه موقعیت زاویهای و ارتباط آن با سایر مفاهیم فیزیکی مثل طول قوس و شعاع، میتوانیم از فرمولهای زیر استفاده کنیم:
![]()
که در آن ![]() موقعیت زاویهای به رادیان است،
موقعیت زاویهای به رادیان است، ![]() طول قوس و
طول قوس و ![]() شعاع دایره است. این فرمول به ما میگوید که زاویهی یک جسم در حرکت دورانی وابسته به مسافتی است که جسم در طول قوس طی میکند و شعاع مسیر حرکت آن.
شعاع دایره است. این فرمول به ما میگوید که زاویهی یک جسم در حرکت دورانی وابسته به مسافتی است که جسم در طول قوس طی میکند و شعاع مسیر حرکت آن.
چرخشهای کامل: تبدیل بین دورها، درجهها و رادیانها
یکی از سوالات رایج در بحث حرکت دورانی این است که چگونه بین دورها (revolutions)، درجهها (degrees) و رادیانها (radians) تبدیل کنیم. همانطور که پیشتر اشاره شد، یک دور کامل برابر با ![]() یا
یا ![]() رادیان است. با این تبدیل ساده، میتوانیم به راحتی زاویهها را بین این سه واحد مختلف تبدیل کنیم.
رادیان است. با این تبدیل ساده، میتوانیم به راحتی زاویهها را بین این سه واحد مختلف تبدیل کنیم.
مثال:
اگر جسمی یک دور کامل بچرخد، موقعیت زاویهای آن چقدر خواهد بود؟
![]()
مثالهای کاربردی از موقعیت زاویهای در زندگی روزمره
برای درک بهتر مفهوم موقعیت زاویهای، چند مثال از زندگی روزمره را بررسی میکنیم.
مثال 1: چرخش عقربه ساعت
فرض کنید عقربه دقیقهشمار یک ساعت در حال چرخش است. اگر این عقربه در طول ۱۵ دقیقه حرکت کند، زاویهای که طی کرده چقدر است؟
- شعاع حرکت این عقربه معادل با فاصله آن از مرکز ساعت است.
- در یک ساعت کامل، عقربه دقیقهشمار یک دور کامل (360°) میچرخد.
بنابراین در 15 دقیقه، عقربه یک چهارم دور کامل چرخیده است. از این\-\-رو:
![]()
این زاویه معادل است با:
![]()
مثال 2: حرکت یک چرخ دنده
فرض کنید یک چرخ دنده با شعاع 10 سانتی متر در حال چرخش است و طول قوس طی شده توسط نقطهای روی محیط چرخ دنده 50 سانتی متر باشد. موقعیت زاویهای این نقطه چقدر خواهد بود؟
برای محاسبه، از فرمول
![]()
استفاده میکنیم:
![]()
بنابراین، زاویهای که این نقطه از چرخ\-\-دنده طی کرده، 5 رادیان است.
مثال 3: ماشین در حال چرخش
فرض کنید تایر یک ماشین در حال چرخش است و ماشین مسافتی معادل ۲۵۰ متر را طی کرده است. اگر شعاع تایر ۰.۵ متر باشد، زاویه چرخش تایر چقدر است؟
ابتدا طول قوس مسیر طیشده توسط نقطهای روی تایر را برابر با مسافت طیشده توسط ماشین فرض میکنیم. بنابراین:
![]()
این به معنای چرخش ۵۰۰ رادیانی تایر است که معادل با چندین دور کامل خواهد بود.
![]()
کاربردهای موقعیت زاویهای در فیزیک
موقعیت زاویهای به طور گستردهای در مباحث مختلف فیزیک و مهندسی کاربرد دارد. برخی از مهمترین کاربردهای آن عبارتاند از:
- مکانیک خودروها: در حرکت چرخشی چرخها و تایرهای خودرو، موقعیت زاویهای نقش حیاتی در اندازهگیری سرعت و مسافت دارد.
- مهندسی مکانیک: در طراحی و تحلیل چرخدندهها و سیستمهای چرخشی.
- هوافضا: در محاسبات حرکت چرخشی ماهوارهها و سفینهها.
تمرینها و سوالات برای درک بهتر
برای درک بهتر مفاهیم مطرحشده، چند سوال تمرینی ارائه میشود:
- اگر یک دیسک در طول ۲ ثانیه ۲ دور کامل بچرخد، موقعیت زاویهای آن چقدر خواهد بود؟
- اگر شعاع یک دایره ۲۰ سانتیمتر باشد و جسمی طول قوسی برابر با ۱۰ سانتیمتر طی کند، موقعیت زاویهای جسم چقدر خواهد بود؟
- چگونه میتوان موقعیت زاویهای یک تایر خودرو را با استفاده از مسافت طیشده توسط خودرو محاسبه کرد؟
پاسخ به تمرینها:
- با استفاده از فرمول
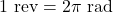 ، برای ۲ دور کامل، موقعیت زاویهای برابر با
، برای ۲ دور کامل، موقعیت زاویهای برابر با 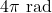 خواهد بود.
خواهد بود. - از فرمول
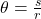 ، داریم
، داریم 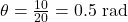 .
. - برای محاسبه، ابتدا طول قوس مسیر طیشده توسط نقطهای روی تایر را به دست آورده و سپس با شعاع تایر آن را تقسیم میکنیم.
جمعبندی
موقعیت زاویهای یکی از مفاهیم کلیدی در حرکت دورانی است که به ما کمک میکند تا وضعیت یک جسم در حال چرخش را توصیف کنیم. با استفاده از مفاهیم ساده و فرمولهای کاربردی، میتوانیم موقعیت زاویهای را در شرایط مختلف محاسبه کنیم. این مفهوم در بسیاری از حوزههای علمی و مهندسی نقش حیاتی دارد و به درک بهتر حرکت اجسام چرخشی کمک میکند.
