توان موج سینوسی در یک ریسمان کشیده
مفهوم توان در فیزیک: محاسبه توان موج سینوسی در یک رشته کشیده
توان (Power) در فیزیک به میزان کار انجامشده یا انرژی منتقلشده در واحد زمان گفته میشود. این مفهوم در بسیاری از شاخههای فیزیک به کار میرود و یکی از مفاهیم کلیدی در فهمیدن چگونگی انتقال انرژی در سیستمهای مختلف است. در این مقاله به توضیح مفهومی و محاسباتی توان متوسط در یک موج سینوسی بر روی یک رشته کشیده میپردازیم. با استفاده از فرمولهای مربوطه و ارائه مثالهای متنوع، این موضوع به زبانی ساده و قابل فهم برای دانشآموزان، دانشجویان، عموم مردم و حتی افراد متخصص توضیح داده میشود.
تعریف توان در فیزیک
توان (Power) به طور کلی به این صورت تعریف میشود:
![]()
که در آن:
![]() توان (بر حسب وات)
توان (بر حسب وات)
![]() انرژی یا کار انجامشده (بر حسب ژول)
انرژی یا کار انجامشده (بر حسب ژول)
![]() زمان (بر حسب ثانیه)
زمان (بر حسب ثانیه)
این معادله به ما نشان میدهد که توان، میزان انتقال انرژی در واحد زمان است. هرچه این مقدار بیشتر باشد، توان بیشتری در سیستم وجود دارد. در سیستمهای مختلف فیزیکی، مانند سیستمهای مکانیکی، الکتریکی، یا موجی، توان یکی از مفاهیم اساسی برای تحلیل نحوه انتقال انرژی است.
تعریف موج سینوسی در رشته کشیده
موج سینوسی یکی از انواع امواج مکانیکی است که در آن ذرات محیط نوسان میکنند و انرژی از نقطهای به نقطه دیگر منتقل میشود. اگر یک رشته کشیده را در نظر بگیریم، موجی که روی آن تولید میشود ممکن است به صورت یک موج سینوسی حرکت کند. چنین امواجی را میتوان با معادله موج توصیف کرد:
![]()
که در آن:
![]() تغییر مکان ذره در نقطهای از رشته و زمانی خاص
تغییر مکان ذره در نقطهای از رشته و زمانی خاص
![]() دامنه موج، یا بیشینه تغییر مکان
دامنه موج، یا بیشینه تغییر مکان
![]() عدد موج (مربوط به طول موج)
عدد موج (مربوط به طول موج)
![]() فرکانس زاویهای (مربوط به بسامد موج)
فرکانس زاویهای (مربوط به بسامد موج)
![]() مکان ذره در طول رشته
مکان ذره در طول رشته
![]() زمان
زمان
این معادله شکل حرکت نوسانی هر نقطه از رشته را توصیف میکند.
توان متوسط موج سینوسی روی یک رشته کشیده
وقتی یک موج سینوسی روی یک رشته کشیده حرکت میکند، انرژی به صورت متناوب بین انرژی پتانسیل و انرژی جنبشی تغییر میکند. این انرژی از یک نقطه به نقطه دیگر منتقل میشود. مقدار توان متوسطی که این موج انتقال میدهد از طریق فرمول زیر محاسبه میشود:
![]()
که در آن:
![]() توان متوسط
توان متوسط
![]() جرم واحد طول رشته (چگالی خطی)
جرم واحد طول رشته (چگالی خطی)
![]() سرعت موج
سرعت موج
![]() فرکانس زاویهای موج
فرکانس زاویهای موج
![]() دامنه موج
دامنه موج
این فرمول به ما نشان میدهد که توان موج به چه عواملی بستگی دارد. مهمترین عوامل شامل جرم واحد طول، سرعت موج، فرکانس زاویهای و دامنه موج هستند. این فرمول بیان میکند که توان با مربع دامنه و مربع فرکانس زاویهای متناسب است. این بدان معناست که افزایش دامنه یا فرکانس موج باعث افزایش توان انتقالی میشود.
تحلیل مفاهیم کلیدی در توان موج سینوسی
1. نقش چگالی خطی (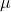 ) در توان موج
) در توان موج
چگالی خطی یا جرم واحد طول یکی از عوامل مهم در انتقال انرژی موج است. چگالی خطی به میزان جرمی که در هر واحد طول رشته وجود دارد، بستگی دارد. هرچه جرم واحد طول بیشتر باشد، انرژی بیشتری برای ایجاد نوسان در رشته نیاز است، که در نتیجه توان بیشتری هم انتقال داده میشود.
2. تأثیر سرعت موج ( ) بر توان
) بر توان
سرعت موج (![]() ) نشاندهنده سرعت انتقال انرژی در طول رشته است. سرعت موج به ویژگیهای فیزیکی رشته مانند کشش و چگالی خطی وابسته است. در واقع، سرعت موج بالاتر به معنای انتقال سریعتر انرژی و افزایش توان است.
) نشاندهنده سرعت انتقال انرژی در طول رشته است. سرعت موج به ویژگیهای فیزیکی رشته مانند کشش و چگالی خطی وابسته است. در واقع، سرعت موج بالاتر به معنای انتقال سریعتر انرژی و افزایش توان است.
3. رابطه فرکانس زاویهای (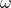 ) و توان
) و توان
فرکانس زاویهای (![]() ) به سرعت نوسان ذرات در طول رشته اشاره دارد. فرکانس بالاتر نشاندهنده افزایش تعداد نوسانات در واحد زمان است. توان انتقالی با مربع فرکانس زاویهای رابطه دارد، بنابراین فرکانس بیشتر به معنای توان بیشتر است.
) به سرعت نوسان ذرات در طول رشته اشاره دارد. فرکانس بالاتر نشاندهنده افزایش تعداد نوسانات در واحد زمان است. توان انتقالی با مربع فرکانس زاویهای رابطه دارد، بنابراین فرکانس بیشتر به معنای توان بیشتر است.
4. دامنه موج (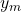 ) و توان
) و توان
دامنه موج (![]() ) نشاندهنده حداکثر تغییر مکان ذرات رشته در هر نوسان است. دامنه بیشتر به معنای جابجایی بیشتر ذرات و در نتیجه انرژی جنبشی و پتانسیل بیشتر است. به همین دلیل، توان انتقالی با مربع دامنه متناسب است.
) نشاندهنده حداکثر تغییر مکان ذرات رشته در هر نوسان است. دامنه بیشتر به معنای جابجایی بیشتر ذرات و در نتیجه انرژی جنبشی و پتانسیل بیشتر است. به همین دلیل، توان انتقالی با مربع دامنه متناسب است.
مثالهای کاربردی از توان موج در رشته کشیده
مثال 1: محاسبه توان متوسط موج در رشته
فرض کنید یک رشته با چگالی خطی ![]() و سرعت موج
و سرعت موج ![]() داریم. دامنه موج
داریم. دامنه موج ![]() و فرکانس زاویهای
و فرکانس زاویهای ![]() است. توان متوسط موج را محاسبه کنید.
است. توان متوسط موج را محاسبه کنید.
ابتدا از فرمول توان متوسط استفاده میکنیم:
![]()
حال مقادیر را جایگذاری میکنیم:
![]()
پس از محاسبه:
![]()
بنابراین توان متوسط موج برابر با ![]() است.
است.
مثال 2: اثر افزایش دامنه بر توان
در مثال قبلی، اگر دامنه موج به جای ![]() به
به ![]() افزایش یابد، توان متوسط چقدر میشود؟
افزایش یابد، توان متوسط چقدر میشود؟
با جایگذاری دامنه جدید در فرمول داریم:
![]()
محاسبه نتیجه میدهد:
![]()
مشاهده میکنیم که با دو برابر شدن دامنه، توان متوسط چهار برابر میشود.
سؤالاتی برای تعامل بیشتر با خواننده
- چگونه میتوان توان انتقالی یک موج را با تغییر در چگالی خطی رشته افزایش داد؟ آیا همیشه افزایش جرم واحد طول به افزایش توان کمک میکند؟
- چه تفاوتی بین سرعت موج در یک رشته کشیده و سرعت موج در محیطهای دیگر، مانند آب یا هوا، وجود دارد؟
- اگر فرکانس موج افزایش یابد ولی دامنه ثابت بماند، چگونه توان انتقالی تغییر خواهد کرد؟
- آیا همیشه افزایش دامنه موج منجر به افزایش توان میشود؟ در چه شرایطی این افزایش ممکن است نامطلوب باشد؟
نتیجهگیری
توان انتقالی توسط یک موج سینوسی در رشته کشیده به عواملی مانند جرم واحد طول، سرعت موج، فرکانس زاویهای و دامنه موج بستگی دارد. با توجه به فرمول توان متوسط، مشخص است که توان با مربع دامنه و مربع فرکانس زاویهای رابطه مستقیم دارد. از این رو، افزایش دامنه یا فرکانس میتواند به طور قابل توجهی توان انتقالی را افزایش دهد.
مفهوم توان در موجهای مکانیکی به ما کمک میکند تا بهتر بفهمیم چگونه انرژی در سیستمهای مختلف منتقل میشود و چگونه میتوان این انتقال انرژی را کنترل یا بهینهسازی کرد. با در نظر گرفتن مثالهای عملی و سؤالاتی که مطرح شد، امیدواریم خوانندگان به درک بهتری از این مفهوم اساسی در فیزیک دست یابند.
