جریان های متناوب و نوسانات واداشته
جریانهای متناوب (AC) و نوسانات اجباری: مدار RLC سری در فیزیک
در دنیای فیزیک و مهندسی، جریانهای متناوب (AC) و نوسانات اجباری یکی از مهمترین مباحثی هستند که در حوزه مدارهای الکتریکی و دینامیک سیستمها مطرح میشوند. این مفاهیم به ما کمک میکنند تا مدارهای پیچیده الکتریکی را درک کرده و رفتار سیستمهای الکتریکی را پیشبینی کنیم. در این مقاله، ما به بررسی یک مدار RLC سری که تحت تأثیر یک نیروی خارجی یا امواج الکتریکی متناوب قرار دارد، میپردازیم. همچنین مفاهیمی مانند فرکانس زاویهای، فاز و نوسانات اجباری را با بیانی ساده و قابل درک توضیح خواهیم داد.
جریان متناوب (AC) چیست؟
جریان الکتریکی به دو نوع اصلی تقسیم میشود: جریان مستقیم (DC) و جریان متناوب (AC). در جریان مستقیم، الکترونها تنها در یک جهت حرکت میکنند، در حالی که در جریان متناوب، جهت حرکت الکترونها بهطور منظم تغییر میکند. یکی از مهمترین مثالهای جریان متناوب، برق شهری است که با فرکانس 50 یا 60 هرتز کار میکند.
مدار RLC چیست؟
یک مدار RLC سری شامل سه عنصر اصلی است:
- مقاومت (R) که نیروی مقاومتکننده در برابر جریان را نشان میدهد.
- خازن (C) که انرژی الکتریکی را ذخیره و تخلیه میکند.
- سلف (L) که انرژی مغناطیسی را ذخیره کرده و تمایل دارد تا تغییرات جریان را متوقف کند.
وقتی یک مدار RLC تحت تأثیر یک نیروی خارجی (مثل جریان متناوب یا یک منبع ولتاژ متناوب) قرار میگیرد، مدار به نوسانات اجباری وارد میشود که در ادامه به آن میپردازیم.
نوسانات اجباری چیست؟
نوسانات اجباری هنگامی رخ میدهند که یک سیستم تحت تأثیر یک نیروی خارجی با فرکانس خاص قرار گیرد. در یک مدار RLC سری، اگر منبع جریان الکتریکی متناوب به مدار وصل شود، ولتاژ و جریان موجود در مدار شروع به نوسان خواهند کرد. این نوسانات به دلیل وجود سلف و خازن در مدار رخ میدهد که به ذخیره و تخلیه انرژی کمک میکنند.
فرکانس زاویهای و امواج سینوسی
در مدارهای AC، ولتاژ متناوب معمولاً بهصورت امواج سینوسی توصیف میشود. یکی از مفاهیم مهم در اینجا فرکانس زاویهای (![]() ) است که به صورت زیر تعریف میشود:
) است که به صورت زیر تعریف میشود:
![]()
در اینجا:
![]() فرکانس زاویهای بر حسب رادیان بر ثانیه است.
فرکانس زاویهای بر حسب رادیان بر ثانیه است.
![]() فرکانس بر حسب هرتز است.
فرکانس بر حسب هرتز است.
امواج سینوسی با معادله زیر بیان میشوند:
![]()
که در آن:
![]() ولتاژ در زمان
ولتاژ در زمان ![]() است.
است.
![]() مقدار حداکثری ولتاژ است.
مقدار حداکثری ولتاژ است.
![]() فرکانس زاویهای جریان هدایتشده توسط منبع ولتاژ خارجی است.
فرکانس زاویهای جریان هدایتشده توسط منبع ولتاژ خارجی است.
رابطه ولتاژ و جریان در مدار RLC
معادله نوسانات اجباری : در یک مدار RLC سری که تحت تأثیر یک نیروی خارجی با فرکانس زاویهای ![]() قرار گرفته است، جریان نیز به صورت موج سینوسی خواهد بود. معادله جریان در مدار به صورت زیر است:
قرار گرفته است، جریان نیز به صورت موج سینوسی خواهد بود. معادله جریان در مدار به صورت زیر است:
![]()
که در آن:
![]() جریان در زمان
جریان در زمان ![]() است.
است.
![]() مقدار حداکثری جریان است.
مقدار حداکثری جریان است.
![]() فرکانس زاویهای نیروی هدایتکننده است.
فرکانس زاویهای نیروی هدایتکننده است.
![]() اختلاف فاز بین جریان و ولتاژ است.
اختلاف فاز بین جریان و ولتاژ است.
اختلاف فاز (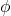 ) در مدار RLC
) در مدار RLC
در مدارهای RLC، جریان و ولتاژ معمولاً دارای اختلاف فاز هستند، یعنی آنها دقیقاً همزمان تغییر نمیکنند. اختلاف فاز به عواملی مانند مقدار مقاومت، سلف و خازن بستگی دارد. به طور کلی، سه حالت ممکن برای اختلاف فاز وجود دارد:
- مدار مقاومتی: در این حالت، اختلاف فاز تقریباً صفر است و ولتاژ و جریان با هم هماهنگ هستند.
- مدار سلفی: در این حالت، ولتاژ پیش از جریان تغییر میکند و اختلاف فاز مثبت است.
- مدار خازنی: در این حالت، جریان پیش از ولتاژ تغییر میکند و اختلاف فاز منفی است.
مثال ساده از اختلاف فاز
تصور کنید شما در حال نوسان دادن به یک تاب هستید. اگر شما دقیقاً در زمان درست نیرویی به تاب وارد کنید، تاب به حداکثر نوسان خود خواهد رسید. اما اگر نیروی شما با تأخیر یا زودتر از زمان مناسب وارد شود، نوسانات تاب ضعیفتر خواهد بود. اختلاف فاز در مدارهای RLC هم مشابه همین مثال است.
امپدانس (Z) در مدار RLC
یکی دیگر از مفاهیم مهم در مدارهای RLC، امپدانس (Z) است. امپدانس مشابه مقاومت در جریان مستقیم است اما در جریانهای متناوب و مدارهای پیچیده مانند مدارهای RLC کاربرد دارد. امپدانس به صورت زیر محاسبه میشود:
![Rendered by QuickLaTeX.com \[Z = \sqrt{R^2 + \left(\omega_d L - \frac{1}{\omega_d C}\right)^2}\]](https://mahmouddehghanpour.com/wp-content/ql-cache/quicklatex.com-515a9b9a96227e1a937bbcce9fcb150e_l3.png)
که در آن:
![]() مقاومت است.
مقاومت است.
![]() سلف است.
سلف است.
![]() خازن است.
خازن است.
![]() فرکانس زاویهای است.
فرکانس زاویهای است.
تأثیر امپدانس در مدار
امپدانس نشاندهنده میزان مقاومت کل مدار در برابر جریان متناوب است. هرچه امپدانس بزرگتر باشد، جریان کمتری از مدار عبور میکند. یکی از حالتهای جالب مدار RLC زمانی رخ میدهد که امپدانس حداقل مقدار خود را داشته باشد؛ این حالت را رزونانس مینامند.
رزنانس در مدار RLC
رزنانس زمانی رخ میدهد که فرکانس نیروی هدایتکننده ![]() برابر با فرکانس طبیعی مدار
برابر با فرکانس طبیعی مدار ![]() شود. در این حالت، مدار به بیشترین مقدار جریان ممکن میرسد و امپدانس حداقل مقدار خود یعنی برابر با مقاومت
شود. در این حالت، مدار به بیشترین مقدار جریان ممکن میرسد و امپدانس حداقل مقدار خود یعنی برابر با مقاومت ![]() میشود. فرکانس طبیعی مدار از رابطه زیر محاسبه میشود:
میشود. فرکانس طبیعی مدار از رابطه زیر محاسبه میشود:
![]()
کاربرد رزنانس
رزنانس در بسیاری از کاربردهای الکتریکی و مهندسی استفاده میشود. برای مثال، در رادیوها و تلویزیونها، مدارهای رزنانس برای انتخاب فرکانسهای خاص از سیگنالهای الکترومغناطیسی استفاده میشوند.
مثال 1: مدار RLC ساده
فرض کنید یک مدار RLC سری دارید که شامل یک مقاومت ![]() ، یک سلف با اندوکتانس
، یک سلف با اندوکتانس ![]() و یک خازن با ظرفیت
و یک خازن با ظرفیت ![]() است. اگر فرکانس زاویهای نیروی هدایتکننده
است. اگر فرکانس زاویهای نیروی هدایتکننده ![]() باشد، امپدانس مدار را محاسبه کنید.
باشد، امپدانس مدار را محاسبه کنید.
حل: ابتدا امپدانس مدار را محاسبه میکنیم:
![Rendered by QuickLaTeX.com \[Z = \sqrt{R^2 + \left(\omega_d L - \frac{1}{\omega_d C}\right)^2}\]](https://mahmouddehghanpour.com/wp-content/ql-cache/quicklatex.com-515a9b9a96227e1a937bbcce9fcb150e_l3.png)
با جایگذاری مقادیر:
![Rendered by QuickLaTeX.com \[Z = \sqrt{(10)^2 + \left((100)(0.5) - \frac{1}{(100)(20 \times 10^{-6})}\right)^2} = \sqrt{100 + (-250)^2} = 250.2 \, \Omega\]](https://mahmouddehghanpour.com/wp-content/ql-cache/quicklatex.com-66feae0c72d1194b279358ee5bc42a62_l3.png)
مثال 2: محاسبه فرکانس رزنانس
در همان مدار، فرکانس طبیعی مدار را محاسبه کنید.
حل: فرکانس رزنانس از رابطه زیر به دست میآید:
![]()
![]()
![]()
بنابراین، فرکانس زاویهای طبیعی مدار برابر با ![]() است.
است.
تفاوت بین جریان و ولتاژ در مدار RLC
همانطور که اشاره شد، در یک مدار RLC سری، بین جریان و ولتاژ اختلاف فاز وجود دارد. بسته به مقادیر سلف، خازن و مقاومت، جریان میتواند پیش از ولتاژ یا بعد از آن به حداکثر خود برسد. بهعنوانمثال:
- اگر مدار غالباً خازنی باشد، جریان پیش از ولتاژ به حداکثر خود میرسد.
- اگر مدار غالباً سلفی باشد، ولتاژ پیش از جریان به حداکثر خود میرسد.
سوالات برای فکر کردن
- سوال 1: اگر یک مدار RLC در حالت رزنانس قرار داشته باشد، چه اتفاقی برای جریان و امپدانس مدار میافتد؟ آیا میتوانید فرکانس رزنانس را برای یک مدار دیگر با مقادیر متفاوت محاسبه کنید؟
- سوال 2: چه عواملی باعث ایجاد اختلاف فاز بین جریان و ولتاژ در مدارهای AC میشود؟ چرا اختلاف فاز در مدارهای خازنی و سلفی متفاوت است؟
- سوال 3: اگر فرکانس زاویهای نیروی هدایتکننده را افزایش دهید، چه تغییری در رفتار مدار RLC مشاهده خواهید کرد؟ آیا به سمت رزنانس نزدیک میشوید یا از آن دور میشوید؟
نکات کلیدی برای درک بهتر مدار RLC
1. درک جریان و ولتاژ
برای درک بهتر رفتار مدار RLC، تصور کنید که جریان و ولتاژ مانند دو دونده در یک مسابقه هستند. اگر مدار در حالت رزنانس باشد، هر دو دونده با سرعت یکسان حرکت میکنند و همزمان به مقصد میرسند (یعنی جریان و ولتاژ تقریباً همزمان تغییر میکنند). اما اگر مدار خازنی یا سلفی باشد، یکی از دوندهها جلوتر از دیگری خواهد بود (یعنی اختلاف فاز وجود دارد).
2. اهمیت امپدانس
امپدانس یکی از مفاهیم کلیدی در مدارهای RLC است. هرگاه بخواهید جریان و ولتاژ را در یک مدار AC پیشبینی کنید، محاسبه امپدانس کمک میکند تا متوجه شوید که چه مقدار جریان از مدار عبور خواهد کرد. به یاد داشته باشید که امپدانس وابسته به فرکانس است، بنابراین با تغییر فرکانس منبع، امپدانس نیز تغییر خواهد کرد.
3. رزنانس و کاربردهای آن
رزنانس یکی از پدیدههای بسیار مهم در مدارهای RLC است که کاربردهای زیادی دارد. مدارهای تنظیمکننده در رادیو و تلویزیون از رزنانس برای انتخاب سیگنالهای خاص استفاده میکنند. همچنین در فیلترهای الکترونیکی از مدارهای رزنانسی برای حذف فرکانسهای ناخواسته استفاده میشود.
نتیجهگیری
در این مقاله، ما به بررسی مفهوم جریان متناوب (AC)، نوسانات اجباری، و رفتار مدار RLC سری پرداختیم. همچنین توضیح دادیم که چگونه فرکانس زاویهای، اختلاف فاز و امپدانس بر رفتار جریان و ولتاژ در این مدار تأثیر میگذارند. یکی از نقاط مهم بحث ما رزنانس بود، که در آن امپدانس به حداقل مقدار خود میرسد و جریان به حداکثر مقدار خود میرسد. درک این مفاهیم به ما کمک میکند تا رفتار سیستمهای پیچیده الکتریکی را درک کنیم و بتوانیم مدارهای الکتریکی را بهینه کنیم.
برای تقویت درک شما از این مباحث، پیشنهاد میکنیم به مثالهای ارائهشده فکر کنید و سوالات مطرحشده را پاسخ دهید. این کار به شما کمک میکند تا ارتباط میان مفاهیم را بهتر درک کرده و کاربردهای آنها را در زندگی روزمره و علوم مهندسی ببینید.
