حرکت پرتابی

حرکت پرتابی: مفهوم، اصول و مثال‌ها

حرکت پرتابی یکی از مباحث بسیار جذاب و کاربردی در فیزیک است که به بررسی مسیر و حرکت اجسامی که به سمت بالا یا زاویه‌دار پرتاب می‌شوند می‌پردازد. این موضوع علاوه بر کاربرد در علوم پایه، در مهندسی، معماری، ورزش و حتی بازی‌های کامپیوتری نیز اهمیت ویژه‌ای دارد. در این مقاله، به صورت جامع و با زبان ساده، به بررسی حرکت پرتابی، فرمول‌های مربوطه، و مثال‌های کاربردی می‌پردازیم تا برای تمامی افراد از دانش‌آموزان گرفته تا متخصصان، قابل درک باشد.

حرکت پرتابی چیست؟ (Projectile Motion)

حرکت پرتابی به حرکت جسمی گفته می‌شود که با یک سرعت اولیه (v₀) پرتاب می‌شود و در طی مسیر خود تحت تاثیر نیروی جاذبه قرار دارد. در این نوع حرکت، شتاب افقی (در راستای محور x) برابر صفر است و تنها شتاب عمودی (در راستای محور y) به دلیل نیروی جاذبه، برابر با g- است.

به زبان ساده‌تر، فرض کنید یک توپ را به سمت بالا پرتاب می‌کنید. این توپ در مسیر خود تحت تاثیر دو عامل قرار دارد:

سرعت اولیه که شما به توپ می‌دهید.
نیروی جاذبه زمین که توپ را به سمت پایین می‌کشد.

این دو عامل باعث می‌شوند که مسیر حرکت توپ به صورت یک سهمی یا همان منحنی پارابولیک باشد.

فرمول‌های حرکت پرتابی

برای تحلیل حرکت پرتابی از چندین فرمول مهم استفاده می‌کنیم که به ما کمک می‌کنند تا مسیر، سرعت، زمان و برد افقی پرتاب جسم را محاسبه کنیم.

معادلات حرکت در راستای افقی و عمودی

معادله حرکت در راستای افقی (x):

$x - x_0 = (v_0 \cos \theta_0) t$

در این فرمول:

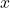$x$ مسافت طی شده در راستای افقی است.
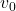$v_0$ سرعت اولیه پرتاب است.
$\theta_0$ زاویه پرتاب با افق است.
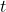$t$ زمان حرکت است.

معادله حرکت در راستای عمودی (y):

$y - y_0 = (v_0 \sin \theta_0) t - \frac{1}{2} g t^2$

این معادله نشان می‌دهد که حرکت در راستای عمودی تحت تاثیر شتاب گرانش (g) قرار دارد.

سرعت عمودی در زمان t:

$v_y = v_0 \sin \theta_0 - gt$

$v_y^2 = (v_0 \sin \theta_0)^2 - 2g(y - y_0)$

در این فرمول:

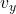$v_y$ سرعت عمودی در هر لحظه است.
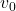$v_0$ سرعت اولیه جسم است.
$\theta_0$ زاویه پرتاب نسبت به افق است.
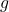$g$ شتاب گرانش زمین است (حدود 9.8 متر بر مجذور ثانیه).
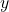$y$ ارتفاع جسم در هر لحظه است.
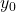$y_0$ ارتفاع اولیه جسم است (در حالت پرتاب از سطح زمین، معمولاً صفر است).

معادله‌ی مسیر :

$y = (x \tan \theta_0) - \frac{g x^2}{2 (v_0 \cos \theta_0)^2}$

این معادله یک مسیر سهمی‌ شکل (پارابولیک) را توصیف می‌کند. در این معادله:

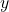$y$ ارتفاع جسم در هر نقطه از مسیر است.
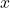$x$ مسافت افقی طی‌شده است.
$\theta_0$ زاویه پرتاب است.
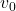$v_0$ سرعت اولیه است.
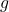$g$ شتاب گرانش است.

برد افقی پرتاب:

$R = \frac{v_0^2}{g} \sin 2\theta_0$

این فرمول برد نهایی پرتاب را محاسبه می‌کند؛ یعنی فاصله افقی که جسم طی می‌کند تا دوباره به ارتفاع اولیه بازگردد.

نکات کلیدی در حرکت پرتابی

زاویه پرتاب ( $\theta_0$ ): زاویه‌ای که جسم با افق می‌سازد، تاثیر مستقیم بر مسیر حرکت و برد جسم دارد. برای مثال، اگر زاویه $45$ درجه باشد، جسم بیشترین برد را خواهد داشت.

شتاب گرانش ( $g$ ): مقدار ثابت $9.8$ متر بر مجذور ثانیه است که همیشه رو به پایین عمل می‌کند.

زمان حرکت ( $t$ ): مدت زمانی که جسم در هوا است نیز وابسته به زاویه پرتاب و سرعت اولیه است.

مثال‌های عملی از حرکت پرتابی

در ادامه به بررسی چند مثال کاربردی از حرکت پرتابی می‌پردازیم تا بهتر با این مفهوم آشنا شویم.

مثال ۱: پرتاب توپ از روی یک سطح صاف

فرض کنید شما توپی را با سرعت اولیه $v_0 = 20 \, \text{m/s}$ و زاویه $30$ درجه نسبت به افق پرتاب می‌کنید. هدف ما این است که برد افقی و حداکثر ارتفاعی که توپ به آن می‌رسد را محاسبه کنیم.

برد افقی را با استفاده از فرمول زیر محاسبه می‌کنیم:

$R = \frac{v_0^2}{g} \sin{2\theta_0}$

با جایگذاری $v_0 = 20 \, \text{m/s}$ ، $g = 9.8 \, \text{m/s}^2$ ، و $\theta_0 = 30^\circ$ ، داریم:

$R = \frac{(20)^2}{9.8} \sin{60^\circ} \approx 35.3 \, \text{m}$

پس برد افقی توپ حدود $35.3$ متر خواهد بود.

مثال ۲: پرتاب شی از ارتفاع

فرض کنید شیئی را از لبه یک ساختمان با ارتفاع ۵۰ متر و زاویه ۴۵ درجه و سرعت اولیه ۱۵ متر بر ثانیه پرتاب می‌کنیم. در اینجا علاوه بر برد افقی، باید زمان حرکت تا برخورد با زمین و همچنین حداکثر ارتفاع جسم را محاسبه کنیم.

ابتدا معادله حرکت عمودی را برای یافتن زمان برخورد با زمین حل می‌کنیم. سپس از زمان برای محاسبه برد افقی استفاده می‌کنیم.

چرا حرکت پرتابی مهم است؟

حرکت پرتابی در زندگی روزمره و صنایع مختلف اهمیت بسیاری دارد. برای مثال:

در مهندسی نظامی برای طراحی مسیر پرتاب موشک‌ها و گلوله‌ها به کار می‌رود.
در ورزش‌هایی مانند فوتبال، بسکتبال و بیسبال برای تعیین مسیر پرتاب توپ‌ها استفاده می‌شود.
حتی در انیمیشن‌ها و بازی‌های ویدیویی نیز برای شبیه‌سازی حرکات طبیعی از این اصول استفاده می‌شود.

سؤالاتی برای تفکر بیشتر

اگر زاویه پرتاب را بیشتر از ۴۵ درجه انتخاب کنیم، چه اتفاقی برای برد جسم خواهد افتاد؟
چگونه می‌توان سرعت اولیه را به گونه‌ای تنظیم کرد که جسم در بیشترین ارتفاع ممکن قرار بگیرد؟
اگر مقاومت هوا در نظر گرفته شود، چه تغییراتی در معادلات حرکت پرتابی به وجود می‌آید؟

نتیجه‌گیری

حرکت پرتابی یکی از مفاهیم مهم و پایه‌ای در فیزیک است که کاربردهای وسیعی در صنایع و زندگی روزمره دارد. با فهمیدن اصول آن و تسلط بر فرمول‌ها، می‌توانیم به تحلیل و پیش‌بینی رفتار اجسام پرتاب‌شده بپردازیم. درک دقیق از این موضوع نه‌تنها در فیزیک بلکه در مهندسی، ورزش و حتی بازی‌های ویدیویی نیز کاربرد دارد. امیدوارم این مقاله شما را در درک بهتر این مفهوم کمک کرده باشد و شما را به تفکر و تحلیل بیشتر در این زمینه ترغیب کند.