سطح صدا در دسی بل
مفهوم سطح صدا در دسیبل (Sound Level in Decibels) و کاربرد آن در فیزیک
در این مقاله به بررسی یکی از مفاهیم مهم فیزیکی یعنی سطح صدا در دسیبل (dB) پرداخته و اصول، فرمولها، و مثالهای کاربردی آن را به زبانی ساده و قابل فهم ارائه میدهیم. این مطلب مناسب دانشآموزان، دانشجویان، عموم مردم و افراد متخصص است. با مطالعه این مقاله، نه تنها با مفهوم سطح صدا آشنا خواهید شد، بلکه خواهید فهمید چگونه این مفهوم در زندگی روزمره و علوم دیگر اهمیت دارد.
سطح صدا چیست؟
قبل از آنکه وارد بحث دقیقتری شویم، بیایید به سادگی توضیح دهیم که سطح صدا به میزان بلندی یا شدتی اشاره دارد که ما از یک منبع صوتی درک میکنیم. برای مثال، صدای صحبت کردن آرام با یک فرد در مقابل صدای بلند موسیقی در یک کنسرت بسیار متفاوت است. سطح صدای هر یک از این دو، بر اساس واحدی به نام دسیبل (decibel) اندازهگیری میشود.
چرا از دسیبل استفاده میکنیم؟
واحد دسیبل برای اندازهگیری صدا به این دلیل استفاده میشود که گوش انسان به طور غیرخطی به صدا واکنش میدهد. این بدان معناست که تغییرات در شدت صدا به صورتی نیست که گوش ما بتواند به صورت خطی آن را حس کند. در نتیجه، به جای استفاده از مقیاس خطی برای اندازهگیری سطح صدا، از مقیاس لگاریتمی استفاده میکنیم که به تغییرات سطح صدا دقیقتر و منطقیتر پاسخ میدهد.
فرمول سطح صدا در دسیبل
سطح صدا در دسیبل با استفاده از فرمول زیر محاسبه میشود:
![]()
در این فرمول:
![]() سطح صدا در واحد دسیبل است.
سطح صدا در واحد دسیبل است.
![]() شدت صدای منبع صوتی (بر حسب وات بر متر مربع، W/m²) است.
شدت صدای منبع صوتی (بر حسب وات بر متر مربع، W/m²) است.
![]() شدت مرجع یا حداقل شدت صدای قابل شنیدن (مقدار
شدت مرجع یا حداقل شدت صدای قابل شنیدن (مقدار ![]() ) است.
) است.
شدت صدای مرجع 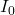
شدت مرجع ![]() برابر است با
برابر است با ![]() که برابر با کمترین شدتی است که گوش انسان قادر به شنیدن آن است. این شدت بسیار کوچک است و عملاً نشاندهنده صدایی است که در حالت عادی نمیشنویم.
که برابر با کمترین شدتی است که گوش انسان قادر به شنیدن آن است. این شدت بسیار کوچک است و عملاً نشاندهنده صدایی است که در حالت عادی نمیشنویم.
مثال کاربردی: مقایسه سطوح مختلف صدا
حال بیایید با استفاده از این فرمول چند مثال ساده و کاربردی ارائه دهیم تا بتوانید مفهوم سطح صدا را بهتر درک کنید.
مثال ۱: صدای نفس کشیدن
شدت صدای نفس کشیدن در حدود ![]() است. با قرار دادن این مقدار در فرمول، سطح صدا را محاسبه میکنیم:
است. با قرار دادن این مقدار در فرمول، سطح صدا را محاسبه میکنیم:
![]()
بنابراین، صدای نفس کشیدن دارای سطح صدای حدود 10 دسیبل است.
مثال ۲: صدای صحبت معمولی
شدت صدای صحبت کردن معمولی در حدود ![]() است. با استفاده از فرمول سطح صدا را محاسبه میکنیم:
است. با استفاده از فرمول سطح صدا را محاسبه میکنیم:
![]()
بنابراین، سطح صدای صحبت کردن معمولی حدود 60 دسیبل است.
مثال ۳: صدای موتور جت
شدت صدای یک موتور جت در حدود ![]() است. با استفاده از فرمول سطح صدا را محاسبه میکنیم:
است. با استفاده از فرمول سطح صدا را محاسبه میکنیم:
![]()
سطح صدای یک موتور جت حدود 120 دسیبل است، که بسیار بلند و نزدیک به آستانه درد انسان است.
اصول فیزیکی مرتبط با سطح صدا
برای درک بهتر مفهوم سطح صدا در دسیبل، باید چند اصل فیزیکی مهم را مرور کنیم.
اصل ۱: شدت صدا و فاصله
یکی از اصول مهم در فیزیک صدا این است که شدت صدا با مجذور فاصله کاهش مییابد. این بدان معناست که هر چه از منبع صوتی دورتر شویم، شدت صدای دریافتی ما به شدت کاهش پیدا میکند. به عنوان مثال، اگر از یک منبع صوتی فاصلهتان دو برابر شود، شدت صدا چهار برابر کاهش مییابد.
اصل ۲: افزایش لگاریتمی سطح صدا
همانطور که فرمول سطح صدا نشان میدهد، افزایش در شدت صدا به صورت لگاریتمی بر سطح صدا تأثیر میگذارد. به عبارت دیگر، هر افزایش ۱۰ برابری در شدت صدا، منجر به افزایش ۱۰ دسیبل در سطح صدا میشود. این باعث میشود که تفاوتهای بزرگ در شدت صدا با استفاده از واحد دسیبل قابل بیان و مقایسه باشند.
اصل ۳: آستانه شنوایی و آستانه درد
گوش انسان قادر است صداهای با شدت های مختلف را بشنود، اما تنها در محدودهای مشخص. آستانه شنوایی کمترین شدت صدایی است که انسان قادر به شنیدن آن است و برابر با ![]() یعنی
یعنی ![]() . از طرف دیگر، آستانه درد، شدت صدایی است که آنقدر بلند است که میتواند به شنوایی انسان آسیب برساند و معمولاً در حدود 120 دسی بل یا بیشتر است.
. از طرف دیگر، آستانه درد، شدت صدایی است که آنقدر بلند است که میتواند به شنوایی انسان آسیب برساند و معمولاً در حدود 120 دسی بل یا بیشتر است.
کاربردهای عملی سطح صدا
مفهوم سطح صدا در دسیبل در بسیاری از جنبههای زندگی روزمره و حرفهای کاربرد دارد. در این بخش به برخی از این کاربردها اشاره میکنیم.
کاربرد ۱: حفاظت از شنوایی
سطوح صدای بالا میتواند به شنوایی آسیب برساند. در محیطهای کاری پر سروصدا مانند کارخانهها یا فرودگاهها، استفاده از تجهیزات حفاظتی گوش ضروری است. سازمانهای بهداشتی معمولاً سطح صدا در محیطهای کاری را محدود میکنند تا کارکنان در معرض صدای بیش از حد بلند قرار نگیرند.
کاربرد ۲: آکوستیک ساختمانها
در طراحی ساختمانها، به ویژه سالنهای کنفرانس، سینماها و تئاترها، مهندسان آکوستیک به دقت سطح صدا و چگونگی انتقال آن را بررسی میکنند تا صدای مطلوب و بدون پژواک به گوش شنوندگان برسد.
کاربرد ۳: صنعت موسیقی
در ضبط و پخش موسیقی، سطح صدای مناسب از اهمیت ویژهای برخوردار است. مهندسان صدا از دسیبل برای تنظیم میکروفنها و تجهیزات صوتی استفاده میکنند تا بهترین کیفیت صدا را ایجاد کنند و از آسیب به تجهیزات جلوگیری شود.
سؤالاتی برای تفکر و تعامل بیشتر
۱. چرا گوش انسان به تغییرات شدت صدا به صورت خطی پاسخ نمیدهد و چرا از مقیاس لگاریتمی برای اندازهگیری سطح صدا استفاده میشود؟
۲. تصور کنید در یک محیط بسیار پر سروصدا مانند یک کنسرت قرار دارید. چطور میتوان شدت صدای کنسرت را کاهش داد بدون اینکه تأثیر آن بر تجربه شنوندگان کم شود؟
۳. اگر بخواهیم سطح صدای یک گفتوگوی آرام را با صدای بلند یک خیابان شلوغ مقایسه کنیم، چه مقدار اختلاف در دسیبل خواهیم داشت و چه عواملی بر درک ما از این اختلاف تأثیر میگذارند؟
نتیجهگیری
سطح صدا در دسیبل یکی از مفاهیم کلیدی در فیزیک صوت است که به ما کمک میکند شدت صداهای مختلف را درک کرده و مقایسه کنیم. استفاده از مقیاس لگاریتمی برای اندازهگیری صدا به دلیل پاسخ غیرخطی گوش انسان به شدت صدا، ضروری است. این مفهوم در زمینههای مختلفی از جمله حفاظت از شنوایی، آکوستیک ساختمانها و صنعت موسیقی کاربرد دارد. امیدواریم با توضیح ساده و مثالهای متنوع، درک بهتری از این مفهوم فیزیکی پیدا کرده باشید و بتوانید آن را در زندگی روزمره یا حرفه خود به کار ببرید.
