شدت در تداخل دو شکاف
مفهوم شدت در تداخل دو شکاف در آزمایش یانگ
تداخل دو شکاف (Two-Slit Interference) یکی از مهمترین پدیدههای علم فیزیک است که به فهم بهتر رفتار امواج کمک میکند. این پدیده برای اولین بار توسط توماس یانگ (Thomas Young) در سال ۱۸۰۱ میلادی مطرح شد. آزمایش او، که به عنوان آزمایش یانگ شناخته میشود، اهمیت زیادی در درک طبیعت موجی نور و امواج دیگر مانند صوت دارد. در این مقاله، ما به بررسی یکی از اصول اساسی این پدیده به نام “شدت” (Intensity) خواهیم پرداخت.
تداخل چیست؟
پیش از ورود به جزئیات شدت در تداخل دو شکاف، لازم است مفهوم تداخل (Interference) را بهطور مختصر مرور کنیم. تداخل زمانی رخ میدهد که دو یا چند موج به یکدیگر برخورد کنند و یک موج جدید ایجاد شود. این پدیده میتواند تداخل سازنده یا تداخل مخرب باشد.
- تداخل سازنده: هنگامی که قلههای دو موج به هم برخورد کنند و یکدیگر را تقویت کنند، ما تداخل سازنده داریم. نتیجهی این تداخل، افزایش دامنهی موج است.
- تداخل مخرب: زمانی که یک قله موج و یک دره موج به هم برخورد کنند و یکدیگر را تضعیف کنند، این حالت تداخل مخرب نامیده میشود و دامنهی موج کاهش مییابد.
حال که این مفاهیم پایهای را مرور کردیم، به بررسی شدت در تداخل دو شکاف در آزمایش یانگ میپردازیم.
شدت (Intensity) در تداخل دو شکاف
در آزمایش یانگ، دو موج از دو شکاف عبور میکنند و در یک صفحه مشاهده (صفحهی نمایش) تداخل ایجاد میکنند. این تداخل به صورت یک سری نوارهای روشن و تاریک (به نام فرنجهای تداخلی) روی صفحه دیده میشود. این نوارهای روشن و تاریک نتیجه تداخل سازنده و مخرب موجها هستند.
یکی از پرسشهای اساسی این است که شدت موج نهایی در نقاط مختلف صفحه مشاهده چگونه محاسبه میشود؟ برای این منظور، از یک رابطهی ریاضی استفاده میکنیم که شدت موج حاصل از تداخل دو موج را توصیف میکند.
فرمول شدت در تداخل دو شکاف
شدت نهایی در صفحه مشاهده از فرمول زیر به دست میآید:
![]()
در این فرمول:
![]() شدت هر یک از دو موج اولیه است.
شدت هر یک از دو موج اولیه است.
![]() تفاوت فاز بین دو موج است.
تفاوت فاز بین دو موج است.
![]() نشاندهنده تغییرات شدت موج با توجه به تفاوت فاز است.
نشاندهنده تغییرات شدت موج با توجه به تفاوت فاز است.
رابطهی فاز 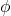
تفاوت فاز بین دو موج ![]() از رابطهی زیر به دست میآید:
از رابطهی زیر به دست میآید:
![]()
که در آن:
![]() فاصله بین دو شکاف است.
فاصله بین دو شکاف است.
![]() زاویهای است که نسبت به مرکز صفحه مشاهده میشود.
زاویهای است که نسبت به مرکز صفحه مشاهده میشود.
![]() طول موج نور یا موج در حال تداخل است.
طول موج نور یا موج در حال تداخل است.
این فرمول به ما کمک میکند تا متوجه شویم چگونه زاویه و فاصله بین شکافها بر تداخل و شدت نوارهای روشن و تاریک تأثیر میگذارند.
توضیح اصول با استفاده از مثالها
بیایید اکنون یک مثال ساده بزنیم تا بهتر متوجه این فرمولها شویم.
مثال ۱: محاسبه شدت در مرکز صفحه مشاهده
فرض کنید در یک آزمایش یانگ، فاصله بین دو شکاف ![]() برابر با ۱ میلیمتر و طول موج
برابر با ۱ میلیمتر و طول موج ![]() برابر با ۵۰۰ نانومتر است. اگر در مرکز صفحه مشاهده (یعنی جایی که زاویه
برابر با ۵۰۰ نانومتر است. اگر در مرکز صفحه مشاهده (یعنی جایی که زاویه ![]() است) شدت تداخل را محاسبه کنیم، چون
است) شدت تداخل را محاسبه کنیم، چون ![]() ، در نتیجه:
، در نتیجه:
![]()
در این حالت، شدت در مرکز صفحه از فرمول زیر محاسبه میشود:
![]()
این نتیجه نشان میدهد که در مرکز صفحه، تداخل کاملاً سازنده است و شدت موج برابر با چهار برابر شدت یکی از امواج اولیه است.
مثال ۲: محاسبه شدت در یک نقطه دیگر
حال فرض کنید بخواهیم شدت موج را در نقطهای محاسبه کنیم که زاویه ![]() برابر با
برابر با ![]() باشد. برای این زاویه، با توجه به اینکه:
باشد. برای این زاویه، با توجه به اینکه:
![]()
و ![]() میلیمتر و
میلیمتر و ![]() نانومتر، مقدار تفاوت فاز
نانومتر، مقدار تفاوت فاز ![]() برابر خواهد بود با:
برابر خواهد بود با:
![]()
اکنون میتوانیم از این تفاوت فاز برای محاسبه شدت استفاده کنیم:
![]()
و چون ![]() است، داریم:
است، داریم:
![]()
این نتیجه نشان میدهد که در این نقطه نیز شدت برابر با چهار برابر شدت یکی از امواج اولیه است.
تعیین نقاط حداکثر و حداقل شدت
یکی از سوالات مهم در آزمایش تداخل این است که نقاطی که در آنها شدت حداکثری (یعنی تداخل سازنده) و شدت حداقلی (یعنی تداخل مخرب) رخ میدهد، کجا هستند.
معادله حداکثر شدت
برای یافتن نقاطی که در آنها شدت حداکثر است، نیاز داریم مقدار ![]() برابر با ۱ باشد. این زمانی رخ میدهد که:
برابر با ۱ باشد. این زمانی رخ میدهد که:
![]()
این معادله به ما کمک میکند تا نقاط حداکثر شدت (یا نوارهای روشن) را پیدا کنیم.
معادله حداقل شدت
برای یافتن نقاط حداقل شدت، باید ![]() باشد. این زمانی رخ میدهد که:
باشد. این زمانی رخ میدهد که:
![]()
این نقاط مکانهایی هستند که شدت به حداقل میرسد (یا نوارهای تاریک).
کاربردهای عملی تداخل دو شکاف
آزمایش تداخل دو شکاف یانگ تنها یک پدیده نظری نیست. این آزمایش و مفاهیم مرتبط با آن در بسیاری از فناوریها و کاربردهای روزمره نقش دارند. از جمله کاربردهای عملی تداخل امواج میتوان به موارد زیر اشاره کرد:
- فیزیک کوانتوم: آزمایش یانگ در فیزیک کوانتوم نیز برای درک دوگانگی موج-ذره استفاده میشود.
- اپتیک: مفاهیم تداخل در طراحی سیستمهای نوری، مانند لنزهای دوربین و میکروسکوپها، کاربرد دارد.
- ارتباطات بیسیم: تداخل امواج در مخابرات بیسیم و طراحی آنتنها مهم است.
سؤالات برای تفکر بیشتر
- چگونه تغییر فاصله بین دو شکاف dd میتواند الگوی تداخل را تغییر دهد؟
- اگر بهجای نور معمولی از نور لیزر استفاده کنیم، الگوی تداخل چه تغییری خواهد کرد؟
- آیا میتوان از امواج دیگر مانند صوت یا آب برای مشاهدهی تداخل دو شکاف استفاده کرد؟ اگر بله، چگونه؟
نتیجهگیری
پدیده تداخل دو شکاف یکی از اصول مهم در علم فیزیک و اپتیک است که به درک ما از طبیعت موجی نور کمک میکند. محاسبه شدت موجهای تداخلی با استفاده از فرمولهای ریاضی به ما امکان میدهد تا بهطور دقیق الگوهای تداخل را تحلیل کنیم. این مفاهیم پایهای نهتنها در کلاسهای فیزیک تدریس میشوند، بلکه در فناوریها و تحقیقات پیشرفته نیز کاربرد دارند.
