متغیرهای خطی و زاویه ای مرتبط
مفاهیم متغیرهای خطی و زاویهای: بررسی نقطهای در یک جسم سفت و چرخشی
در علم فیزیک، درک ارتباط بین حرکت خطی و حرکت زاویهای برای توصیف حرکت اجسام چرخشی امری بسیار مهم است. این مقاله با زبانی ساده و توضیحاتی روشن به مفهوم متغیرهای خطی و زاویهای در اجسام چرخشی میپردازد و این مفاهیم را به کمک مثالها و فرمولهای کاربردی برای دانشآموزان، دانشجویان و عموم مردم قابل درک میسازد.
متغیرهای خطی و زاویهای در حرکت چرخشی
حرکت چرخشی یا دورانی یکی از انواع اصلی حرکت است که در زندگی روزمره به وفور مشاهده میشود؛ از چرخش زمین به دور محور خود گرفته تا چرخش چرخهای اتومبیل. درک حرکت چرخشی به دو متغیر اصلی وابسته است: متغیرهای زاویهای و متغیرهای خطی. این متغیرها به ما کمک میکنند تا حرکت هر نقطه در یک جسم چرخشی را توصیف کنیم. اما تفاوتها و ارتباطهای این دو نوع متغیر چیست؟ و چگونه میتوان آنها را به یکدیگر مرتبط ساخت؟
تعریف حرکت زاویهای و حرکت خطی
وقتی یک جسم به دور محور خود میچرخد، هر نقطه از آن جسم به صورت دایرهای حرکت میکند. این حرکت دایرهای با استفاده از متغیرهای زاویهای توصیف میشود. نقطهای که در فاصله شعاعی rr از محور چرخش قرار دارد، در یک دایره با شعاع rr حرکت میکند. اما همین نقطه، علاوه بر حرکت زاویهای، حرکت خطی هم دارد. این حرکت خطی همان مسیری است که نقطه طی میکند تا در طول دایره حرکت کند. این ارتباط بین متغیرهای زاویهای و خطی موضوع اصلی این مقاله است.
حرکت زاویهای: معرفی مفهوم زاویه و سرعت زاویهای
زاویه 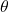 و طول کمان
و طول کمان 
زاویه ![]() یک متغیر کلیدی در حرکت زاویهای است که مقدار چرخش جسم را مشخص میکند. اگر جسمی به اندازه زاویه
یک متغیر کلیدی در حرکت زاویهای است که مقدار چرخش جسم را مشخص میکند. اگر جسمی به اندازه زاویه ![]() (برحسب رادیان) چرخش کند، نقطهای که در فاصله
(برحسب رادیان) چرخش کند، نقطهای که در فاصله ![]() از محور چرخش قرار دارد، روی یک کمان به طول
از محور چرخش قرار دارد، روی یک کمان به طول ![]() حرکت خواهد کرد. فرمول زیر این ارتباط را نشان میدهد:
حرکت خواهد کرد. فرمول زیر این ارتباط را نشان میدهد:
![]()
در این فرمول:
![]() : طول کمان (برحسب متر)
: طول کمان (برحسب متر)
![]() : زاویه چرخش (برحسب رادیان)
: زاویه چرخش (برحسب رادیان)
![]() : فاصله نقطه از محور چرخش یا شعاع دایره (برحسب متر)
: فاصله نقطه از محور چرخش یا شعاع دایره (برحسب متر)
مثال:
فرض کنید یک چرخه در حال چرخش است و چرخش آن به اندازه ![]() رادیان باشد. اگر شعاع چرخ
رادیان باشد. اگر شعاع چرخ ![]() متر باشد، طول کمانی که یک نقطه روی لبه چرخ طی میکند برابر است با:
متر باشد، طول کمانی که یک نقطه روی لبه چرخ طی میکند برابر است با:
![]()
این بدان معنی است که نقطه لبه چرخ در اثر چرخش، 1 متر در دایرهای با شعاع 0.5 متر حرکت کرده است.
سرعت زاویهای 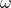
سرعت زاویهای یا همان ![]() نشاندهنده سرعت چرخش جسم حول محور چرخش است. اگر جسم در زمان
نشاندهنده سرعت چرخش جسم حول محور چرخش است. اگر جسم در زمان ![]() زاویه
زاویه ![]() را طی کند، سرعت زاویهای آن به شکل زیر تعریف میشود:
را طی کند، سرعت زاویهای آن به شکل زیر تعریف میشود:
![]()
در این فرمول:
![]() : سرعت زاویهای (برحسب رادیان بر ثانیه)
: سرعت زاویهای (برحسب رادیان بر ثانیه)
![]() : زاویه چرخش (برحسب رادیان)
: زاویه چرخش (برحسب رادیان)
![]() : زمان چرخش (برحسب ثانیه)
: زمان چرخش (برحسب ثانیه)
مثال:
فرض کنید چرخی در مدت ![]() ثانیه به اندازه
ثانیه به اندازه ![]() رادیان چرخش کرده باشد. سرعت زاویهای این چرخ به شکل زیر محاسبه میشود:
رادیان چرخش کرده باشد. سرعت زاویهای این چرخ به شکل زیر محاسبه میشود:
![]()
این بدان معناست که چرخ با سرعت زاویهای 1.5 رادیان بر ثانیه میچرخد.
حرکت خطی: سرعت و شتاب در حرکت دایرهای
سرعت خطی 
هر نقطه در یک جسم چرخشی علاوه بر حرکت زاویهای، حرکت خطی نیز دارد. سرعت خطی ![]() یک نقطه روی یک دایره با شعاع
یک نقطه روی یک دایره با شعاع ![]() به سرعت زاویهای جسم مرتبط است. این رابطه به صورت زیر بیان میشود:
به سرعت زاویهای جسم مرتبط است. این رابطه به صورت زیر بیان میشود:
![]()
در این فرمول:
![]() : سرعت خطی (برحسب متر بر ثانیه)
: سرعت خطی (برحسب متر بر ثانیه)
![]() : سرعت زاویهای (برحسب رادیان بر ثانیه)
: سرعت زاویهای (برحسب رادیان بر ثانیه)
![]() : شعاع دایره (برحسب متر)
: شعاع دایره (برحسب متر)
مثال:
فرض کنید یک چرخه با سرعت زاویهای ![]() رادیان بر ثانیه در حال چرخش است و شعاع چرخ برابر با
رادیان بر ثانیه در حال چرخش است و شعاع چرخ برابر با ![]() متر باشد. سرعت خطی یک نقطه روی لبه چرخ به شکل زیر محاسبه میشود:
متر باشد. سرعت خطی یک نقطه روی لبه چرخ به شکل زیر محاسبه میشود:
![]()
این نشان میدهد که نقطهای روی لبه چرخ با سرعت 1.2 متر بر ثانیه در حرکت است.
شتاب خطی و شتاب زاویهای
شتاب خطی به دو بخش تقسیم میشود: شتاب مماسی و شتاب مرکزی (رادیال).
شتاب مماسی 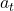
شتاب مماسی به تغییر سرعت خطی نقطه در طول زمان اشاره دارد و به شتاب زاویهای ![]() مرتبط است:
مرتبط است:
![]()
در این فرمول:
![]() : شتاب مماسی (برحسب متر بر ثانیه مربع)
: شتاب مماسی (برحسب متر بر ثانیه مربع)
![]() : شتاب زاویهای (برحسب رادیان بر ثانیه مربع)
: شتاب زاویهای (برحسب رادیان بر ثانیه مربع)
![]() : شعاع دایره (برحسب متر)
: شعاع دایره (برحسب متر)
مثال:
اگر چرخشی با شتاب زاویهای ![]() رادیان بر ثانیه مربع و شعاع
رادیان بر ثانیه مربع و شعاع ![]() متر داشته باشیم، شتاب مماسی نقطه روی لبه چرخ به صورت زیر محاسبه میشود:
متر داشته باشیم، شتاب مماسی نقطه روی لبه چرخ به صورت زیر محاسبه میشود:
![]()
شتاب مرکزی 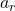
شتاب مرکزی یا رادیال ناشی از تغییر جهت سرعت خطی است و به صورت زیر تعریف میشود:
![]()
این شتاب به سمت مرکز دایره است و به سرعت خطی و شعاع دایره وابسته است.
مثال:
اگر سرعت زاویهای چرخ برابر با ![]() رادیان بر ثانیه و شعاع دایره
رادیان بر ثانیه و شعاع دایره ![]() متر باشد، شتاب رادیال به صورت زیر محاسبه میشود:
متر باشد، شتاب رادیال به صورت زیر محاسبه میشود:
![]()
دوره تناوب و فرکانس در حرکت دایرهای
یکی دیگر از مفاهیم کلیدی در حرکت چرخشی، دوره تناوب ![]() و فرکانس
و فرکانس ![]() است. دوره تناوب مدت زمانی است که جسم برای یک دور کامل به دور محور خود صرف میکند و فرمول آن به شکل زیر است:
است. دوره تناوب مدت زمانی است که جسم برای یک دور کامل به دور محور خود صرف میکند و فرمول آن به شکل زیر است:
![]()
در حالی که فرکانس به تعداد دورهایی اشاره دارد که جسم در هر ثانیه طی میکند و به شکل زیر تعریف میشود:
![]()
سؤالاتی برای تفکر بیشتر
- چگونه میتوان سرعت خطی یک نقطه را در یک جسم چرخشی بدون استفاده از سرعت زاویهای محاسبه کرد؟
- اگر سرعت زاویهای جسمی دو برابر شود، چه تغییری در شتاب مماسی و شتاب مرکزی رخ میدهد؟
- در چه شرایطی شتاب مماسی و شتاب رادیال برابر میشوند؟
- آیا میتوان نقطهای روی یک جسم چرخشی را تصور کرد که سرعت خطی آن صفر باشد؟ چرا؟
