مدارهای سری RL

آشنایی با مدارهای سری RL: مفاهیم، فرمول‌ها و مثال‌ها

مدارهای سری RL یکی از مهم‌ترین و پرکاربردترین مدارهای الکتریکی هستند که در آن‌ها مقاومت (R) و القا (L) به صورت سری به یک منبع ولتاژ متصل می‌شوند. در این مدارها، وقتی یک نیروی محرکه الکتریکی ثابت (ℰ) به مدار وارد می‌شود، جریان به‌تدریج افزایش می‌یابد تا به یک مقدار تعادل برسد. همین‌طور، هنگامی‌که منبع ولتاژ قطع می‌شود، جریان به‌تدریج کاهش می‌یابد و از مدار خارج می‌شود. درک این فرآیندها برای دانش‌آموزان و علاقه‌مندان به فیزیک می‌تواند چالش‌برانگیز باشد، اما با استفاده از مثال‌ها و توضیحات ساده می‌توان به مفاهیم اساسی پی برد.

مدار سری RL چیست؟

مدار سری RL مداری است که از دو عنصر اصلی تشکیل شده است: یک مقاومت (R) و یک سلف یا القاگر (L) که به یکدیگر متصل شده و به منبع ولتاژ (ام‌اف یا emf) وصل می‌شوند. هدف از مطالعه این مدارها، درک رفتار جریان الکتریکی در شرایط مختلف (روشن و خاموش شدن منبع ولتاژ) است.

مقاومت (R)

مقاومت عنصری است که مانع حرکت جریان الکتریکی در مدار می‌شود. به‌عبارتی، مقاومت مقدار جریانی را که می‌تواند از مدار عبور کند، کاهش می‌دهد.

سلف یا القاگر (L)

سلف عنصری است که در برابر تغییرات جریان مقاومت نشان می‌دهد. به‌عبارت دیگر، سلف تمایل دارد که جریان مدار را ثابت نگه دارد و مانع از تغییرات ناگهانی در جریان شود.

رفتار جریان در مدار سری RL

هنگامی‌که یک نیروی محرکه ثابت (ℰ) به مدار اعمال می‌شود، جریان به‌آرامی افزایش می‌یابد و به مقدار تعادل خود می‌رسد. این رفتار به دلیل وجود القاگر در مدار است که تغییرات ناگهانی جریان را محدود می‌کند. همچنین، وقتی منبع ولتاژ قطع می‌شود، جریان نیز به‌آرامی کاهش می‌یابد تا به صفر برسد. برای درک بهتر این موضوع، فرمول‌های اساسی مرتبط با این مدار را بررسی می‌کنیم.

افزایش جریان در مدار سری RL

هنگامی‌که منبع ولتاژ به مدار وصل می‌شود، جریان به‌آرامی از صفر به یک مقدار تعادل می‌رسد. این فرآیند طبق فرمول زیر توصیف می‌شود:

$i(t) = \frac{E}{R} \left(1 - e^{-\frac{t}{\tau_L}}\right)$

در اینجا:

$i(t)$ جریان در زمان $t$ است.
$E$ نیروی محرکه الکتریکی (EMF) ثابت است.
$R$ مقاومت مدار است.
$\tau_L = \frac{L}{R}$ ثابت زمانی القایی مدار است که از نسبت القا به مقاومت به دست می‌آید.
این فرمول نشان می‌دهد که جریان به تدریج به مقدار $\frac{E}{R}$ نزدیک می‌شود. برای مثال، اگر $R = 10 \, \Omega$ و $L = 5 \, H$ باشد، و منبع ولتاژ $E = 50 \, V$ به مدار اعمال شود، جریان پس از گذشت مدت‌زمانی به مقدار $\frac{50}{10} = 5 \, A$ می‌رسد.

کاهش جریان در مدار سری RL

وقتی منبع ولتاژ قطع می‌شود، جریان موجود در مدار به‌آرامی کاهش می‌یابد و طبق فرمول زیر از مقدار اولیه $i_0$ به صفر میل می‌کند:

$i(t) = i_0 e^{-\frac{t}{\tau_L}}$

در اینجا:

$i_0$ مقدار اولیه جریان هنگام قطع ولتاژ است.
$\tau_L$ همان ثابت زمانی القایی مدار است.

این فرمول نشان می‌دهد که چگونه جریان به‌آرامی و با گذشت زمان به صفر کاهش می‌یابد. به‌عبارتی، کاهش جریان در مدار سری RL هیچ‌گاه ناگهانی نیست، بلکه به‌صورت نمایی انجام می‌شود.

ثابت زمانی القایی (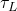 $\tau_L$ ) چیست؟

ثابت زمانی القایی یکی از مفاهیم کلیدی در مدارهای سری RL است که نشان‌دهنده سرعت تغییر جریان در مدار است. هرچه ثابت زمانی بزرگ‌تر باشد، تغییرات جریان آهسته‌تر انجام می‌شود. این ثابت از نسبت القا $L$ به مقاومت $R$ محاسبه می‌شود:

$\tau_L = \frac{L}{R}$

به‌عنوان مثال، اگر القای مدار $L = 4 \, H$ و مقاومت $R = 2 \, \Omega$ باشد، ثابت زمانی برابر با $4/2 = 2$ ثانیه خواهد بود. این به این معنی است که بعد از گذشت 2 ثانیه، جریان مدار تقریباً به 63 درصد مقدار نهایی خود می‌رسد.

مثال‌هایی برای درک بهتر

برای درک بهتر مفاهیم مدار سری RL، به چند مثال عملی توجه کنید:

مثال 1: افزایش جریان در مدار سری RL

فرض کنید یک مدار سری RL شامل یک مقاومت $R = 10 \, \Omega$ و یک القاگر $L = 2 \, H$ است. اگر یک نیروی محرکه $E = 20 \, V$ به مدار اعمال شود، جریان مدار چگونه افزایش می‌یابد؟

با استفاده از فرمول افزایش جریان:

$i(t) = \frac{E}{R} \left(1 - e^{-\frac{t}{\tau_L}}\right)$

ابتدا ثابت زمانی $\tau_L$ را محاسبه می‌کنیم:

$\tau_L = \frac{L}{R} = \frac{2}{10} = 0.2 \text{ ثانیه}$

پس از گذشت 0.2 ثانیه، جریان به حدود 63 درصد مقدار نهایی خود یعنی $\frac{20}{10} = 2 \, A$ می‌رسد.

مثال 2: کاهش جریان در مدار سری RL

حال فرض کنید در همان مدار، جریان به مقدار $i_0 = 3 A$ رسیده باشد و سپس منبع ولتاژ قطع شود. جریان مدار پس از 0.4 ثانیه چقدر خواهد بود؟

با استفاده از فرمول کاهش جریان:

$i(t) = i_0 e^{-\frac{t}{\tau_L}}$

با جایگذاری مقادیر:

$i(0.4) = 3 e^{-\frac{0.4}{0.2}} = 3 e^{-2} \approx 3 \times 0.135 = 0.405 A$

پس از 0.4 ثانیه، جریان مدار به حدود 0.405 آمپر کاهش می‌یابد.

اهمیت مدارهای سری RL در دنیای واقعی

مدارهای سری RL در بسیاری از کاربردهای عملی استفاده می‌شوند. یکی از کاربردهای اصلی این مدارها در مدارهای فیلتر است که برای فیلتر کردن سیگنال‌های ناخواسته در سیستم‌های الکترونیکی استفاده می‌شوند. همچنین، مدارهای سری RL در موتورهای الکتریکی و ترانسفورماتورها نقش کلیدی ایفا می‌کنند، جایی که کنترل جریان و مدیریت تغییرات آن اهمیت ویژه‌ای دارد.

سؤالاتی برای تفکر بیشتر

برای تقویت درک مفاهیم مدار سری RL، به چند سؤال زیر فکر کنید:

چرا در مدارهای سری RL جریان نمی‌تواند به‌طور ناگهانی به مقدار نهایی خود برسد؟
چگونه تغییر مقاومت یا القا بر روی ثابت زمانی 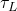$\tau_L$ و سرعت تغییر جریان تأثیر می‌گذارد؟
در کدام کاربردهای عملی دیگر می‌توانیم از مدارهای سری RL استفاده کنیم؟
چه تفاوتی میان مدارهای سری RL و مدارهای دیگر مانند RC (مقاومت-خازن) وجود دارد؟

نتیجه‌گیری

مدارهای سری RL به دلیل ترکیب مقاومت و القا، یکی از مدارهای مهم در الکترونیک و فیزیک محسوب می‌شوند. درک رفتار جریان در این مدارها، چه در هنگام افزایش جریان و چه در هنگام کاهش آن، به دانش‌آموزان کمک می‌کند تا مفاهیم پیچیده‌تری مانند القای الکتریکی و ذخیره انرژی در میدان‌های مغناطیسی را بهتر بفهمند. با استفاده از فرمول‌های ساده و مثال‌های کاربردی، می‌توان به‌راحتی این مفاهیم را درک کرد و از آن‌ها در کاربردهای عملی استفاده نمود.