موج رونده
موجهای مسافرتی: تعریف، اصول و معادله حرکت موج
موجهای مسافرتی پدیدههای اساسی در علم فیزیک هستند که به ما کمک میکنند رفتار امواج را در محیطهای مختلف توضیح دهیم. درک دقیق این امواج و معادلههای مربوطه، برای دانشآموزان، دانشجویان، و حتی متخصصین حوزههای فیزیک و مهندسی اهمیت بسیاری دارد. در این مقاله، به زبان ساده به توضیح مفهوم “معادله موج مسافرتی” میپردازیم و مفاهیم مرتبط را با مثالهای متنوع و توضیحات کاربردی توضیح میدهیم.
مفهوم اولیه موج
برای شروع، بیایید ابتدا نگاهی به تعریف موج بیندازیم. موج به انتقال انرژی از یک نقطه به نقطه دیگر بدون انتقال ماده گفته میشود. برای مثال، اگر یک سنگ را به درون یک دریاچه بیندازید، امواجی روی سطح آب ایجاد میشوند که انرژی را از نقطهای که سنگ وارد آب شده، به اطراف منتقل میکنند، اما خود آب به عنوان ماده، به طور عمده از جای خود حرکت نمیکند.
امواج میتوانند به دو دسته کلی تقسیم شوند:
- امواج مکانیکی: مانند امواج صوتی یا امواج روی سطح آب که برای انتشار نیاز به یک محیط مادی دارند.
- امواج الکترومغناطیسی: مانند نور که نیازی به محیط ندارند و میتوانند در خلاء منتشر شوند.
در این مقاله بیشتر به نوع اول، یعنی امواج مکانیکی و بهویژه امواج مسافرتی، خواهیم پرداخت.
معادله موج مسافرتی چیست؟
معادله موج مسافرتی بهصورت کلی به شکل زیر بیان میشود:
![]()
در این معادله:
![]() : مکان موج در زمان
: مکان موج در زمان ![]() و مکان
و مکان ![]() است.
است.
![]() : شکل ریاضی موج است که با تابع
: شکل ریاضی موج است که با تابع ![]() مشخص میشود.
مشخص میشود.
![]() : عدد موج است که به موج طولی یا فرکانس زاویهای ارتباط دارد.
: عدد موج است که به موج طولی یا فرکانس زاویهای ارتباط دارد.
![]() : فرکانس زاویهای موج است که سرعت تناوب زمانی موج را مشخص میکند.
: فرکانس زاویهای موج است که سرعت تناوب زمانی موج را مشخص میکند.
![]() : مختصات مکانی.
: مختصات مکانی.
![]() : زمان.
: زمان.
علامت + نشان دهنده موجی است که در جهت منفی محور ![]() حرکت میکند.
حرکت میکند.
علامت – نشان دهنده موجی است که در جهت مثبت محور ![]() حرکت میکند.
حرکت میکند.
این معادله، برای هر نوع موجی که به صورت مسافرتی در محیطی خاص حرکت میکند، صدق میکند.
نکته کلیدی:
موج مسافرتی نوعی موج است که به صورت پیوسته در یک جهت خاص (مثبت یا منفی) حرکت میکند. این حرکت به گونهای است که شکل موج بدون تغییر میماند و تنها مکان موج به مرور زمان جابهجا میشود.
توضیح اصول و مؤلفههای معادله موج مسافرتی
۱. تابع 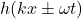 چیست؟
چیست؟
تابع ![]() شکل موج را توصیف میکند. این تابع میتواند هر شکلی داشته باشد: مثلاً یک سینوسی ساده، یا حتی یک پالس مربعی یا مثلثی. در واقع، این تابع مشخص میکند که شکل فیزیکی موج در هر نقطه از زمان و مکان چگونه است.
شکل موج را توصیف میکند. این تابع میتواند هر شکلی داشته باشد: مثلاً یک سینوسی ساده، یا حتی یک پالس مربعی یا مثلثی. در واقع، این تابع مشخص میکند که شکل فیزیکی موج در هر نقطه از زمان و مکان چگونه است.
برای مثال، اگر شکل موج یک تابع سینوسی باشد:
![]()
در اینجا ![]() دامنه موج است که نشان دهنده حداکثر جابجایی موج از وضعیت تعادلش است. چنین موجی شکل یک موج سینوسی خواهد داشت و به صورت مسافرتی در جهت مثبت
دامنه موج است که نشان دهنده حداکثر جابجایی موج از وضعیت تعادلش است. چنین موجی شکل یک موج سینوسی خواهد داشت و به صورت مسافرتی در جهت مثبت ![]() حرکت میکند.
حرکت میکند.
۲. عدد موج 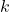 چیست؟
چیست؟
عدد موج که با نماد ![]() نشان داده میشود، به شکل هندسی موج اشاره دارد و با طول موج رابطه معکوس دارد. این عدد به صورت زیر تعریف میشود:
نشان داده میشود، به شکل هندسی موج اشاره دارد و با طول موج رابطه معکوس دارد. این عدد به صورت زیر تعریف میشود:
![]()
که در آن ![]() طول موج است. هرچه طول موج کوتاهتر باشد، عدد موج بزرگتر است و برعکس.
طول موج است. هرچه طول موج کوتاهتر باشد، عدد موج بزرگتر است و برعکس.
۳. فرکانس زاویهای 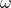 چیست؟
چیست؟
فرکانس زاویهای موج، تعداد دورهایی است که موج در واحد زمان در یک مکان مشخص طی میکند. این فرکانس به صورت زیر تعریف میشود:
![]()
که در آن ![]() فرکانس موج (به واحد هرتز) است.
فرکانس موج (به واحد هرتز) است.
۴. سرعت موج
سرعت موج رابطهای با فرکانس و طول موج دارد. سرعت موج را میتوان با استفاده از فرمول زیر محاسبه کرد:
![]()
این فرمول نشان میدهد که سرعت موج تابعی از فرکانس زاویهای و عدد موج است. برای امواج مکانیکی، سرعت موج به ویژگیهای محیط انتقال بستگی دارد، مثلاً سرعت صوت در هوا با سرعت آن در آب متفاوت است.
جهت حرکت موج
یکی از نکات مهم در معادله موج مسافرتی، علامت مثبت یا منفی در تابع است. این علامت جهت حرکت موج را تعیین میکند. اگر:
علامت مثبت باشد (![]() ): موج در جهت منفی محور
): موج در جهت منفی محور ![]() حرکت میکند.
حرکت میکند.
علامت منفی باشد (![]() ): موج در جهت مثبت محور
): موج در جهت مثبت محور ![]() حرکت میکند.
حرکت میکند.
سؤال:
آیا میتوانید خودتان به این فکر کنید که چگونه سرعت موج و جهت حرکت آن با ویژگیهای محیطی مانند چگالی محیط ارتباط دارد؟
مثالهای کاربردی برای معادله موج مسافرتی
۱. موج صوتی
فرض کنید یک موج صوتی در هوا در حال حرکت است. موج\u200cهای صوتی، امواج مکانیکی طولی هستند که از طریق تراکم و انبساط مولکول\u200cهای هوا انتقال می\u200cیابند. معادله حرکت موج صوتی می\u200cتواند به صورت زیر نوشته شود:
![]()
در اینجا، ![]() نشان دهنده شدت صدا است (دامنه موج)،
نشان دهنده شدت صدا است (دامنه موج)، ![]() عدد موج و
عدد موج و ![]() فرکانس زاویه\u200cای است. با حرکت موج در زمان
فرکانس زاویه\u200cای است. با حرکت موج در زمان ![]() ، شکل موج به صورت سینوسی در فضا منتشر می\u200cشود.
، شکل موج به صورت سینوسی در فضا منتشر می\u200cشود.
۲. موج روی سطح آب
یک موج ساده روی سطح آب نیز می تواند به صورت زیر توصیف شود:
![]()
در این مثال، موج در جهت منفی محور ![]() حرکت می کند. این موج با گذشت زمان در سطح آب پخش شده و حرکت می کند.
حرکت می کند. این موج با گذشت زمان در سطح آب پخش شده و حرکت می کند.
سؤال:
چرا سرعت موج صوتی در هوا با سرعت موج روی سطح آب متفاوت است؟ چه عواملی در این تفاوت دخیل هستند؟
تأثیر محیط بر حرکت موج
همانطور که اشاره شد، سرعت حرکت موج به محیطی که موج در آن حرکت میکند، بستگی دارد. برای مثال، سرعت صوت در هوا حدود 343 متر بر ثانیه است، در حالی که در آب سرعت آن بیشتر از 1500 متر بر ثانیه است. این تفاوت به دلیل ویژگیهای فیزیکی مانند چگالی و سختی محیط است.
سؤال:
آیا میتوانید به این فکر کنید که چگونه تغییر دما میتواند بر سرعت امواج صوتی تأثیر بگذارد؟
تمرین و تفکر
برای درک بهتر معادله موج مسافرتی، به چند سؤال توجه کنید و سعی کنید آنها را پاسخ دهید:
- اگر فرکانس یک موج افزایش یابد، چه تأثیری بر سرعت آن خواهد داشت؟
- چرا امواج الکترومغناطیسی نیازی به محیط مادی برای انتشار ندارند؟
- چگونه میتوانیم معادله موج مسافرتی را برای یک موج نوری در نظر بگیریم؟
- چه عواملی ممکن است باعث تغییر در دامنه موج شوند؟
نکته نهایی:
مفهوم موج مسافرتی یکی از مفاهیم بنیادین در فیزیک است که در بسیاری از پدیدههای طبیعی کاربرد دارد. درک دقیق معادله موج مسافرتی به ما کمک میکند تا رفتار امواج را بهتر بفهمیم و در بسیاری از زمینههای علمی و صنعتی از این دانش بهره بگیریم.
