میدان مغناطیسی یک قوس دایره ای
میدان مغناطیسی یک قوس دایرهای: مفاهیم و کاربردها
مفهوم میدان مغناطیسی یکی از مهمترین موضوعات در علم فیزیک است که کاربردهای گستردهای دارد. در این مقاله قصد داریم با زبانی ساده و مثالهای متنوع به بررسی یکی از حالتهای خاص میدان مغناطیسی یعنی میدان مغناطیسی ناشی از یک قوس دایرهای بپردازیم. درک صحیح این موضوع میتواند به دانشجویان فیزیک، مهندسان و حتی علاقهمندان به علم کمک کند تا با پدیدههای مغناطیسی بهطور عمیقتری آشنا شوند.
مفهوم میدان مغناطیسی
میدان مغناطیسی ناحیهای از فضا است که در آن یک نیروی مغناطیسی بر روی ذرات باردار و یا دیگر مواد مغناطیسی وارد میشود. این میدانها معمولاً به وسیله جریانهای الکتریکی یا مواد مغناطیسی ایجاد میشوند. یکی از روشهای کلیدی برای تولید میدان مغناطیسی، عبور جریان الکتریکی از یک سیم است. حال بیایید به حالتی خاصتر از این پدیده، یعنی میدان مغناطیسی ناشی از یک قوس دایرهای بپردازیم.
تعریف میدان مغناطیسی در مرکز قوس دایرهای
فرض کنید یک سیم به شکل یک قوس دایرهای خم شده و جریان الکتریکی ![]() از آن عبور میکند. هدف ما محاسبه میدان مغناطیسی
از آن عبور میکند. هدف ما محاسبه میدان مغناطیسی ![]() در مرکز این قوس است. میدان مغناطیسی در چنین وضعیتی بهصورت تجربی و با استفاده از قوانین الکترومغناطیس قابل محاسبه است.
در مرکز این قوس است. میدان مغناطیسی در چنین وضعیتی بهصورت تجربی و با استفاده از قوانین الکترومغناطیس قابل محاسبه است.
برای یک قوس دایرهای به شعاع ![]() و زاویه مرکزی
و زاویه مرکزی ![]() (بر حسب رادیان)، فرمول میدان مغناطیسی در مرکز قوس به صورت زیر است:
(بر حسب رادیان)، فرمول میدان مغناطیسی در مرکز قوس به صورت زیر است:
![]()
که در آن:
![]() میدان مغناطیسی در مرکز قوس است.
میدان مغناطیسی در مرکز قوس است.
![]() ثابت تراوایی خلأ (با مقدار تقریبی
ثابت تراوایی خلأ (با مقدار تقریبی ![]() تسلا-متر بر آمپر).
تسلا-متر بر آمپر).
![]() جریان الکتریکی در سیم است.
جریان الکتریکی در سیم است.
![]() زاویه مرکزی قوس (بر حسب رادیان).
زاویه مرکزی قوس (بر حسب رادیان).
![]() شعاع قوس.
شعاع قوس.
چرا میدان مغناطیسی در مرکز یک قوس دایرهای اهمیت دارد؟
این موضوع از آن جهت اهمیت دارد که بسیاری از دستگاهها و ابزارهایی که با جریان الکتریکی کار میکنند، به میدان مغناطیسی وابسته هستند. درک نحوه محاسبه میدان مغناطیسی در اشکال مختلف سیمها، مانند قوس دایرهای، به ما کمک میکند تا نحوه عملکرد ابزارهایی مانند ژنراتورها و موتورهای الکتریکی را بهتر بفهمیم. همچنین، محاسبه میدان مغناطیسی به طراحان مدارهای الکتریکی این امکان را میدهد تا دستگاههای کارآمدتر و کمهزینهتری بسازند.
تجزیه و تحلیل فرمول: تأثیر پارامترها بر میدان مغناطیسی
بیایید به بررسی دقیقتر هر یک از اجزای فرمول میدان مغناطیسی بپردازیم.
نقش زاویه مرکزی 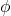
زاویه مرکزی قوس، میزان انحنای قوس را مشخص میکند. هرچه این زاویه بزرگتر باشد، میدان مغناطیسی قویتری در مرکز قوس تولید میشود. به عبارت دیگر، اگر قوس به دایره کامل نزدیکتر شود (زاویه مرکزی به ![]() برسد)، میدان مغناطیسی نیز قویتر خواهد شد. اما اگر زاویه مرکزی کم باشد، میدان مغناطیسی ضعیفتری خواهیم داشت.
برسد)، میدان مغناطیسی نیز قویتر خواهد شد. اما اگر زاویه مرکزی کم باشد، میدان مغناطیسی ضعیفتری خواهیم داشت.
برای مثال، اگر زاویه ![]() برابر با
برابر با ![]() (90 درجه) باشد، میدان مغناطیسی کمتر از حالتی است که زاویه برابر با
(90 درجه) باشد، میدان مغناطیسی کمتر از حالتی است که زاویه برابر با ![]() (180 درجه) باشد.
(180 درجه) باشد.
نقش شعاع 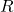
شعاع قوس نیز تأثیر مستقیمی بر میدان مغناطیسی دارد. هرچه شعاع بزرگتر باشد، میدان مغناطیسی ضعیفتر خواهد بود. این به این دلیل است که فاصله بین نقطهای که میدان مغناطیسی محاسبه میشود (مرکز قوس) و جریان الکتریکی بیشتر میشود و این باعث کاهش تأثیر میدان میشود.
برای مثال، اگر شعاع ![]() دو برابر شود، میدان مغناطیسی به نصف کاهش مییابد.
دو برابر شود، میدان مغناطیسی به نصف کاهش مییابد.
نقش جریان 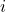
میدان مغناطیسی با جریان الکتریکی مستقیم نسبت دارد. هرچه جریان بیشتری از سیم عبور کند، میدان مغناطیسی قویتری در مرکز قوس تولید میشود. به همین دلیل، در دستگاههایی که نیاز به میدان مغناطیسی قوی دارند، جریانهای بزرگتری استفاده میشود.
ثابت تراوایی خلأ 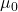
ثابت ![]() نشاندهنده ویژگیهای مغناطیسی فضای خلأ است. این ثابت در همه جا مقدار یکسانی دارد و نقش مهمی در محاسبات میدان مغناطیسی دارد. اگر مادهای با ویژگیهای مغناطیسی متفاوت در فضا وجود داشته باشد، این ثابت تغییر میکند، اما در اغلب موارد، از
نشاندهنده ویژگیهای مغناطیسی فضای خلأ است. این ثابت در همه جا مقدار یکسانی دارد و نقش مهمی در محاسبات میدان مغناطیسی دارد. اگر مادهای با ویژگیهای مغناطیسی متفاوت در فضا وجود داشته باشد، این ثابت تغییر میکند، اما در اغلب موارد، از ![]() برای محاسبات استفاده میکنیم.
برای محاسبات استفاده میکنیم.
مثالها برای درک بهتر
برای درک بهتر فرمول میدان مغناطیسی، چند مثال ساده و کاربردی را بررسی میکنیم:
مثال 1: محاسبه میدان مغناطیسی برای یک قوس نیمدایرهای
فرض کنید یک سیم به شکل نیمدایره با شعاع ![]() و جریان
و جریان ![]() داشته باشیم. زاویه مرکزی این نیمدایره برابر با
داشته باشیم. زاویه مرکزی این نیمدایره برابر با ![]() است. حال میخواهیم میدان مغناطیسی در مرکز این نیمدایره را محاسبه کنیم.
است. حال میخواهیم میدان مغناطیسی در مرکز این نیمدایره را محاسبه کنیم.
با استفاده از فرمول:
![]()
در نتیجه، میدان مغناطیسی در مرکز این نیمدایره برابر با ![]() تسلا خواهد بود.
تسلا خواهد بود.
مثال 2: تأثیر تغییر زاویه مرکزی
فرض کنید همان قوس دایرهای مثال قبل را داشته باشیم، اما این بار زاویه قوس برابر با ![]() (90 درجه) باشد. میدان مغناطیسی در این حالت چقدر خواهد بود؟
(90 درجه) باشد. میدان مغناطیسی در این حالت چقدر خواهد بود؟
با استفاده از فرمول:
![]()
همانطور که مشاهده میکنید، میدان مغناطیسی به دلیل کاهش زاویه قوس، نصف حالت قبلی شده است.
مثال 3: تأثیر تغییر شعاع
حال فرض کنید همان قوس نیمدایرهای را داریم، اما شعاع آن به ![]() تغییر میکند. میدان مغناطیسی در این حالت چقدر خواهد بود؟
تغییر میکند. میدان مغناطیسی در این حالت چقدر خواهد بود؟
![]()
میدان مغناطیسی با افزایش شعاع به نصف مقدار اولیه کاهش یافته است.
سؤالاتی برای تأمل و درک بیشتر
1. اگر زاویه قوس به ![]() برسد (یعنی سیم به شکل دایره کامل درآید)، میدان مغناطیسی در مرکز چگونه تغییر میکند؟
برسد (یعنی سیم به شکل دایره کامل درآید)، میدان مغناطیسی در مرکز چگونه تغییر میکند؟
2. چگونه میتوان با استفاده از چندین قوس دایرهای میدان مغناطیسی قویتری در مرکز ایجاد کرد؟
3. در صورتی که به جای سیمی با یک جریان، از چندین سیم موازی با جریانهای یکسان استفاده کنیم، میدان مغناطیسی در مرکز چگونه تحت تأثیر قرار میگیرد؟
4. آیا این فرمول تنها برای قوسهای دایرهای در هوا معتبر است یا در محیطهای دیگری هم قابل استفاده است؟
