کار انجامشده توسط نیروی فنر
کار انجامشده توسط نیروی فنر: راهنمای جامع و کاربردی
در علم فیزیک، مفهوم کار (Work) یکی از پایههای اساسی برای درک حرکت و نیرو است. یکی از حالتهای خاص از این مفهوم، کار انجامشده توسط نیروی فنر است. در این مقاله بهعنوان یک استاد فیزیک با تجربه، قصد داریم این مفهوم را با زبانی ساده و قابلفهم توضیح دهیم و با ارائه مثالهای متعدد، به شما کمک کنیم تا درک عمیقی از آن پیدا کنید. این مقاله برای دانشآموزان، دانشجویان، عموم مردم و حتی متخصصان فیزیک مفید خواهد بود. همچنین سوالات تفکری در طول مقاله مطرح میشود تا شما را به تعامل بیشتر با مطالب وادارد.
مفهوم نیروی فنر چیست؟
برای شروع، بیایید نیروی فنر را تعریف کنیم. فنرها وسیلههایی هستند که نیرویی مخالف جهت کشیده شدن یا فشرده شدن خود ایجاد میکنند. این نیرو به نیروی بازگشتی یا نیروی الاستیک معروف است. قانون هوک این نیرو را بهطور دقیق توصیف میکند.
قانون هوک (Hooke’s Law)
قانون هوک بیان میکند که نیروی بازگشتی ![]() که یک فنر به جسم متصل به آن وارد میکند، متناسب با تغییر طول فنر از حالت تعادل است. این رابطه بهصورت زیر بیان میشود:
که یک فنر به جسم متصل به آن وارد میکند، متناسب با تغییر طول فنر از حالت تعادل است. این رابطه بهصورت زیر بیان میشود:
![]()
در این رابطه:
![]() نیروی بازگشتی فنر است.
نیروی بازگشتی فنر است.
![]() ثابت فنر است که سختی فنر را نشان میدهد.
ثابت فنر است که سختی فنر را نشان میدهد.
![]() جابجایی فنر از حالت تعادل است (فاصلهای که فنر کشیده یا فشرده شده است).
جابجایی فنر از حالت تعادل است (فاصلهای که فنر کشیده یا فشرده شده است).
علامت منفی نشاندهنده این است که جهت نیروی بازگشتی فنر، مخالف جهت تغییر طول فنر است.
تعریف کار انجامشده توسط نیروی فنر
حالا که نیروی فنر را شناختیم، به سراغ مفهوم “کار انجامشده توسط نیروی فنر” میرویم. وقتی جسمی به انتهای آزاد فنری متصل است و فنر کشیده یا فشرده میشود، نیروی بازگشتی فنر کاری روی جسم انجام میدهد. این کار میتواند مثبت یا منفی باشد، بسته به اینکه جسم در جهت یا خلاف جهت نیروی فنر حرکت کند.
فرمول کار انجامشده توسط نیروی فنر
کار انجامشده توسط نیروی فنر از رابطه زیر بدست میآید:
![]()
در این فرمول:
![]() کار انجامشده توسط نیروی فنر است.
کار انجامشده توسط نیروی فنر است.
![]() ثابت فنر است.
ثابت فنر است.
![]() موقعیت اولیه جسم (طول اولیه فنر) است.
موقعیت اولیه جسم (طول اولیه فنر) است.
![]() موقعیت نهایی جسم (طول نهایی فنر) است.
موقعیت نهایی جسم (طول نهایی فنر) است.
حالت خاص: وقتی 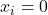
یکی از حالتهای رایج این است که جسم از حالت تعادل فنر (![]() ) به موقعیت جدیدی
) به موقعیت جدیدی ![]() منتقل شود. در این صورت، فرمول کار انجامشده توسط نیروی فنر بهصورت زیر ساده میشود:
منتقل شود. در این صورت، فرمول کار انجامشده توسط نیروی فنر بهصورت زیر ساده میشود:
![]()
این رابطه نشان میدهد که کار انجامشده توسط نیروی فنر همیشه منفی است، زیرا جهت نیروی فنر مخالف جهت حرکت جسم است.
اصول و مفاهیم کلیدی
۱. نیروی فنر یک نیروی محافظهکار است
نیروی فنر یک نیروی محافظهکار است، به این معنی که کار انجامشده توسط این نیرو تنها به موقعیت اولیه و نهایی جسم بستگی دارد و مسیری که طی شده است اهمیتی ندارد. به عبارت دیگر، انرژیای که در فنر ذخیره میشود، تابعی از تغییر طول فنر است.
۲. انرژی پتانسیل الاستیک
کار انجامشده توسط نیروی فنر ارتباط نزدیکی با مفهوم “انرژی پتانسیل الاستیک” دارد. وقتی فنر کشیده یا فشرده میشود، انرژی درون آن ذخیره میشود. این انرژی ذخیرهشده به عنوان انرژی پتانسیل الاستیک شناخته میشود و مقدار آن از رابطه زیر محاسبه میشود:
![]()
که ![]() انرژی پتانسیل الاستیک و
انرژی پتانسیل الاستیک و ![]() میزان تغییر طول فنر از حالت تعادل است.
میزان تغییر طول فنر از حالت تعادل است.
۳. کار انجامشده در جهات مختلف
اگر جسم در جهت نیروی فنر حرکت کند، کار انجامشده منفی خواهد بود زیرا نیروی فنر در جهت مخالف حرکت جسم است. اما اگر نیروی خارجی باعث کشیدن فنر شود، کار انجامشده توسط نیروی خارجی مثبت است.
مثالهای کاربردی از کار نیروی فنر
برای درک بهتر این مفهوم، به چند مثال ساده و کاربردی میپردازیم.
مثال ۱: کشیدن یک فنر
فرض کنید یک فنر با ثابت فنر ![]() به یک جسم متصل شده است. جسم از حالت تعادل به اندازه
به یک جسم متصل شده است. جسم از حالت تعادل به اندازه ![]() کشیده میشود. کار انجامشده توسط نیروی فنر را محاسبه کنید.
کشیده میشود. کار انجامشده توسط نیروی فنر را محاسبه کنید.
راهحل:
با استفاده از فرمول:
![]()
![]()
بنابراین، کار انجامشده توسط نیروی فنر برابر با ![]() است.
است.
مثال ۲: فشردن یک فنر
فرض کنید فنری با ثابت ![]() به اندازه
به اندازه ![]() فشرده شده است. انرژی پتانسیل الاستیک ذخیرهشده در این فنر چقدر است؟
فشرده شده است. انرژی پتانسیل الاستیک ذخیرهشده در این فنر چقدر است؟
راهحل:
با استفاده از فرمول انرژی پتانسیل الاستیک:
![]()
![]()
بنابراین، انرژی پتانسیل الاستیک ذخیرهشده برابر با ![]() است.
است.
مثال ۳: حرکت جسم متصل به فنر
یک جسم با جرم ![]() به انتهای یک فنر با ثابت
به انتهای یک فنر با ثابت ![]() متصل است. جسم به اندازه
متصل است. جسم به اندازه ![]() از حالت تعادل خود کشیده میشود. سرعت جسم در لحظه عبور از حالت تعادل چقدر خواهد بود؟
از حالت تعادل خود کشیده میشود. سرعت جسم در لحظه عبور از حالت تعادل چقدر خواهد بود؟
راهحل:
در اینجا، از قانون پایستگی انرژی استفاده میکنیم. انرژی پتانسیل فنر به انرژی جنبشی جسم تبدیل میشود:
![]()
با جایگذاری مقادیر:
![]()
![]()
بنابراین، سرعت جسم در لحظه عبور از حالت تعادل برابر با ![]() است.
است.
سوالاتی برای تفکر بیشتر
اگر فنری با ثابت ![]() به اندازه
به اندازه ![]() فشرده شود، چقدر انرژی پتانسیل در آن ذخیره میشود؟
فشرده شود، چقدر انرژی پتانسیل در آن ذخیره میشود؟
۲. در صورتی که نیرویی خارجی باعث کشیدن یک فنر شود، کار انجامشده توسط نیروی خارجی چه تفاوتی با کار انجامشده توسط نیروی فنر خواهد داشت؟
۳. آیا ممکن است کار انجامشده توسط نیروی فنر مثبت باشد؟ در چه شرایطی این اتفاق میافتد؟
۴. اگر فنری بهطور ناگهانی آزاد شود، انرژی پتانسیل ذخیرهشده چگونه به انرژی جنبشی تبدیل میشود؟ آیا میتوان رابطهای بین این دو یافت؟
نتیجهگیری
در این مقاله، مفهوم “کار انجامشده توسط نیروی فنر” را به زبانی ساده و با استفاده از فرمولها و مثالهای کاربردی بررسی کردیم. با یادگیری این مفاهیم، شما توانستید درک بهتری از نیروهای بازگشتی، انرژی پتانسیل الاستیک و کار مکانیکی پیدا کنید. امیدواریم که این مقاله برای شما مفید و قابلاستفاده بوده باشد.
