کار انجام شده توسط نیروی گرانشی
کار انجام شده توسط نیروی گرانشی (Work Done by the Gravitational Force)
در فیزیک، مفهوم «کار» به انرژی منتقل شده به یا از یک جسم در اثر اعمال نیرو در طول مسافت گفته میشود. یکی از مهمترین نیروهایی که در زندگی روزمره ما همواره با آن سر و کار داریم، نیروی گرانشی است. نیروی گرانش یا همان جاذبه زمین، نیرویی است که زمین بر تمامی اجسام وارد میکند. این مقاله به بررسی دقیق مفهوم کار انجام شده توسط نیروی گرانشی و چگونگی محاسبه آن با استفاده از فرمولهای ساده میپردازد. در این مقاله با استفاده از توضیحات ساده و مثالهای کاربردی به بیان این مفهوم خواهیم پرداخت تا مخاطبان مختلف از جمله دانشآموزان، دانشجویان و حتی متخصصین بتوانند از آن بهرهمند شوند.
کار چیست؟
در علم فیزیک، کار زمانی انجام میشود که نیرویی به جسم وارد شود و آن جسم در جهت نیرو جابجا شود. به عبارت دیگر، کار زمانی انجام میشود که انرژی از یک سیستم به سیستم دیگر منتقل شود. فرمول کلی کار به صورت زیر است:
![]()
که در آن:
![]() کار انجام شده (به ژول)
کار انجام شده (به ژول)
![]() نیروی وارد شده (به نیوتون)
نیروی وارد شده (به نیوتون)
![]() مسافتی که جسم در جهت نیرو جابجا میشود (به متر)
مسافتی که جسم در جهت نیرو جابجا میشود (به متر)
![]() زاویه بین جهت نیرو و جهت جابجایی جسم است.
زاویه بین جهت نیرو و جهت جابجایی جسم است.
نیروی گرانشی چیست؟
نیروی گرانشی نیرویی است که بین دو جسم با جرم وجود دارد. این نیرو همیشه به سمت مرکز جرم اجسام عمل میکند. بر روی سطح زمین، این نیرو به صورت عمودی و رو به پایین (به سمت مرکز زمین) وارد میشود و اندازه آن برابر است با:
![]()
که در آن:
![]() نیروی گرانشی
نیروی گرانشی
![]() جرم جسم (به کیلوگرم)
جرم جسم (به کیلوگرم)
![]() شتاب گرانشی زمین است که مقدار آن تقریباً
شتاب گرانشی زمین است که مقدار آن تقریباً ![]() است.
است.
کار انجام شده توسط نیروی گرانشی
کار انجام شده توسط نیروی گرانشی زمانی مطرح میشود که جسمی تحت تأثیر نیروی گرانشی از نقطهای به نقطه دیگر جابجا شود. برای محاسبه کار انجام شده توسط این نیرو، از فرمول زیر استفاده میشود:
![]()
در این فرمول:
![]() کار انجام شده توسط نیروی گرانشی
کار انجام شده توسط نیروی گرانشی
![]() جرم جسم
جرم جسم
![]() شتاب گرانش
شتاب گرانش
![]() جابجایی جسم
جابجایی جسم
![]() زاویه بین نیروی گرانش و جهت جابجایی جسم.
زاویه بین نیروی گرانش و جهت جابجایی جسم.
حالت های مختلف زاویه 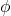
- اگر زاویه
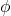 صفر باشد: به این معنی است که جابجایی جسم دقیقاً در جهت نیروی گرانشی است (به سمت پایین). در این حالت،
صفر باشد: به این معنی است که جابجایی جسم دقیقاً در جهت نیروی گرانشی است (به سمت پایین). در این حالت،
![Rendered by QuickLaTeX.com \[\cos(0) = 1\]](https://mahmouddehghanpour.com/wp-content/ql-cache/quicklatex.com-aeb2b5a79245f49cf0a6916a15911a18_l3.png)
، بنابراین:
![Rendered by QuickLaTeX.com \[W_g = mgd\]](https://mahmouddehghanpour.com/wp-content/ql-cache/quicklatex.com-df88d9cf4e4afafa7fbb46213d94c4e6_l3.png)
- اگر زاویه
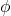 90 درجه باشد: به این معنی است که جسم به صورت افقی حرکت می کند و جابجایی آن عمود بر جهت نیروی گرانشی است. در این حالت،
90 درجه باشد: به این معنی است که جسم به صورت افقی حرکت می کند و جابجایی آن عمود بر جهت نیروی گرانشی است. در این حالت،
![Rendered by QuickLaTeX.com \[\cos(90^\circ) = 0\]](https://mahmouddehghanpour.com/wp-content/ql-cache/quicklatex.com-118e89894d729732f6bd7f6859e780a2_l3.png)
، بنابراین:
![Rendered by QuickLaTeX.com \[W_g = 0\]](https://mahmouddehghanpour.com/wp-content/ql-cache/quicklatex.com-0804a4a5825c34e2daf630cda2d6dba8_l3.png)
در این حالت، نیروی گرانش هیچ کاری روی جسم انجام نمی دهد.
- اگر زاویه
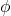 180 درجه باشد: یعنی جسم در خلاف جهت نیروی گرانشی (به سمت بالا) حرکت می کند. در این حالت،
180 درجه باشد: یعنی جسم در خلاف جهت نیروی گرانشی (به سمت بالا) حرکت می کند. در این حالت،
![Rendered by QuickLaTeX.com \[\cos(180^\circ) = -1\]](https://mahmouddehghanpour.com/wp-content/ql-cache/quicklatex.com-c60ee2f2c682029596085c9c82a51e83_l3.png)
، بنابراین:
![Rendered by QuickLaTeX.com \[W_g = -mgd\]](https://mahmouddehghanpour.com/wp-content/ql-cache/quicklatex.com-b5a25724527e5a0ad56116c8b7176aa1_l3.png)
کار منفی نشان دهنده این است که انرژی از سیستم خارج می شود، یا به عبارت دیگر، انرژی به جسم اضافه نمی شود.
مثالهای کاربردی
مثال ۱: سقوط آزاد جسم
فرض کنید یک توپ با جرم ![]() kg از ارتفاع
kg از ارتفاع ![]() m به زمین رها میشود. کار انجام شده توسط نیروی گرانشی در طول این جابجایی چقدر است؟
m به زمین رها میشود. کار انجام شده توسط نیروی گرانشی در طول این جابجایی چقدر است؟
![]() kg,
kg, ![]() m/s
m/s![]() ,
, ![]() m,
m, ![]()
از فرمول کار گرانشی داریم:
![]()
بنابراین، کار انجام شده توسط نیروی گرانشی ![]() J است.
J است.
مثال ۲: حرکت افقی جسم
حال فرض کنید همان توپ ![]()
![]() به صورت افقی در سطح صاف به مسافت
به صورت افقی در سطح صاف به مسافت ![]()
![]() جابجا میشود. کار انجام شده توسط نیروی گرانشی در این حالت چقدر است؟
جابجا میشود. کار انجام شده توسط نیروی گرانشی در این حالت چقدر است؟
در اینجا زاویه ![]() است، بنابراین:
است، بنابراین:
![]()
در نتیجه، نیروی گرانشی در این حرکت افقی هیچ کاری انجام نمیدهد.
مثال ۳: بالا بردن جسم
فرض کنید همان توپ را به ارتفاع ![]()
![]() بالا میبرید. کار انجام شده توسط نیروی گرانشی در این حالت چقدر است؟
بالا میبرید. کار انجام شده توسط نیروی گرانشی در این حالت چقدر است؟
![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
از فرمول داریم:
![]()
کار منفی نشان میدهد که انرژی از جسم گرفته شده است و برای غلبه بر نیروی گرانش انرژی مصرف شده است.
سؤالاتی برای تفکر بیشتر
چگونه میتوان کار نیروی گرانشی را در حرکات منحنی محاسبه کرد؟ آیا همیشه از فرمول ساده
![]()
میتوان استفاده کرد یا شرایط خاصی نیاز به تحلیل دقیقتری دارد؟
چرا نیروی گرانشی در حرکتهای افقی کاری انجام نمیدهد؟ آیا این موضوع در تمامی شرایط درست است یا استثناهایی وجود دارد؟
اگر جسمی در خلا حرکت کند، آیا همچنان نیروی گرانشی بر آن تأثیر میگذارد؟ اگر پاسخ مثبت است، چگونه میتوان کار گرانشی را در این حالت محاسبه کرد؟
جمع بندی
در این مقاله به بررسی مفهوم «کار انجام شده توسط نیروی گرانشی» پرداختیم. نیروی گرانشی نیرویی است که زمین به اجسام وارد میکند و میتواند در جهت های مختلف کار مثبت یا منفی انجام دهد. فرمول کار انجام شده توسط نیروی گرانشی به صورت
![]()
بیان می شود که در آن زاویه بین نیرو و جهت جابجایی نقش مهمی در محاسبه کار دارد. مثال های ارائه شده نشان میدهند که چگونه میتوان این مفهوم را در حالات مختلف به کار برد.
در نهایت، این مفاهیم علاوه بر کاربرد در مسائل ساده، پایهای برای درک بیشتر در مباحث پیشرفته تر فیزیک مانند مکانیک سیالات، ترمودینامیک و حتی فیزیک کوانتومی هستند.
