گشتاور زاویه ای مداری و گشتاور دوقطبی مغناطیسی
گشتاور زاویهای مداری و گشتاور دوقطبی مغناطیسی: مفاهیم پایهای در فیزیک
گشتاور زاویهای مداری (Orbital Angular Momentum) و گشتاور دوقطبی مغناطیسی (Magnetic Dipole Moment) از جمله مفاهیم کلیدی در فیزیک کوانتومی هستند که برای درک بهتر ساختار اتمها و رفتار ذرات زیراتمی مانند الکترونها ضروریاند. این مفاهیم به دانشجویان، دانشآموزان و علاقهمندان به فیزیک کمک میکند تا شناخت دقیقی از نحوه حرکت و ویژگیهای ذرات در سطح اتمی پیدا کنند. در این مقاله، به صورت ساده و جامع به توضیح این مفاهیم میپردازیم و برای روشنتر شدن موضوع، فرمولها، اصول و مثالهایی ارائه میکنیم.
مفهوم گشتاور زاویهای مداری
گشتاور زاویهای چیست؟ گشتاور زاویهای (Angular Momentum) در فیزیک به معنای تمایل یک جسم چرخان برای ادامه دادن به حرکت چرخشی خود است. این مفهوم مشابه مومنتوم خطی (حرکت مستقیم) است، اما برای حرکتهای چرخشی استفاده میشود. هر جسمی که به دور یک محور میچرخد، دارای گشتاور زاویهای است که به جرم، سرعت و فاصله آن از محور چرخش بستگی دارد.
اما در سطح اتمی و کوانتومی، گشتاور زاویهای مداری معنای خاصی پیدا میکند. الکترونهایی که در اتمها به دور هسته میچرخند، به دلیل این حرکت، دارای گشتاور زاویهای مداری هستند. این گشتاور زاویهای با قوانین کوانتومی توضیح داده میشود که در آن مقادیر گسسته و کوانتیزهای دارد.
تعریف گشتاور زاویهای مداری الکترون
در فیزیک کوانتومی، گشتاور زاویهای مداری الکترون در یک اتم به صورت زیر تعریف میشود:
![]()
در اینجا:
![]() عدد کوانتومی مداری است که مقادیر آن از 0 تا
عدد کوانتومی مداری است که مقادیر آن از 0 تا ![]() متغیر است، که در آن
متغیر است، که در آن ![]() عدد کوانتومی اصلی الکترون است.
عدد کوانتومی اصلی الکترون است.
![]() مقدار ثابت پلانک تقسیم بر
مقدار ثابت پلانک تقسیم بر ![]() است که به صورت عددی تقریباً برابر
است که به صورت عددی تقریباً برابر ![]() است.
است.
این فرمول نشان میدهد که مقدار گشتاور زاویهای مداری کوانتیزه است و نمیتواند هر مقداری داشته باشد. به طور خاص، مقادیر گشتاور زاویهای مداری الکترون در مقادیر مشخص و گسستهای قرار میگیرد.
مثال ساده
فرض کنید یک الکترون در یک لایه با عدد کوانتومی اصلی ![]() قرار داشته باشد. در این حالت، مقادیر ممکن برای
قرار داشته باشد. در این حالت، مقادیر ممکن برای ![]() میتواند 0، 1 یا 2 باشد. حال اگر
میتواند 0، 1 یا 2 باشد. حال اگر ![]() باشد، مقدار گشتاور زاویهای مداری به صورت زیر خواهد بود:
باشد، مقدار گشتاور زاویهای مداری به صورت زیر خواهد بود:
![]()
این یعنی الکترون در این حالت دارای گشتاور زاویهای مداری معینی است که از قانون کوانتومی تبعیت میکند.
مولفههای گشتاور زاویهای روی محور z
در سیستمهای کوانتومی، علاوه بر کل گشتاور زاویهای، مؤلفههای گشتاور زاویهای روی یک محور خاص مانند محور zz نیز اهمیت دارند. این مولفه، با رابطه زیر بیان میشود:
![]()
در اینجا:
![]() عدد کوانتومی مغناطیسی مداری است که مقادیر آن از
عدد کوانتومی مغناطیسی مداری است که مقادیر آن از ![]() تا
تا ![]() تغییر میکند (یعنی
تغییر میکند (یعنی ![]() ).
).
مثال ساده
اگر ![]() باشد، مقادیر ممکن برای
باشد، مقادیر ممکن برای ![]() برابر است با
برابر است با ![]() . فرض کنید
. فرض کنید ![]() باشد، در این صورت مقدار
باشد، در این صورت مقدار ![]() به صورت زیر خواهد بود:
به صورت زیر خواهد بود:
![]()
این یعنی مؤلفه گشتاور زاویهای الکترون روی محور zz برابر با یک مقدار مشخص است که باز هم کوانتیزه است.
گشتاور دوقطبی مغناطیسی الکترون
گشتاور دوقطبی مغناطیسی چیست؟ گشتاور دوقطبی مغناطیسی (Magnetic Dipole Moment) به تمایل یک جسم باردار برای ایجاد میدان مغناطیسی گفته میشود. در مورد الکترونها، به دلیل حرکت مداری و اسپین، الکترونها گشتاور دوقطبی مغناطیسی دارند که این امر باعث تولید میدان مغناطیسی میشود.
گشتاور دوقطبی مغناطیسی مداری الکترون، به صورت زیر تعریف میشود:
![]()
در اینجا:
![]() بار الکترون است که مقدار آن
بار الکترون است که مقدار آن ![]() است.
است.
![]() جرم الکترون است که مقدار آن تقریباً
جرم الکترون است که مقدار آن تقریباً ![]() است.
است.
![]() عدد کوانتومی مداری الکترون است.
عدد کوانتومی مداری الکترون است.
مولفه گشتاور مغناطیسی روی محور z
همچنین مؤلفه گشتاور مغناطیسی روی محور ![]() نیز به صورت زیر کوانتیزه است:
نیز به صورت زیر کوانتیزه است:
![]()
که در آن ![]() بور مغناطون است و مقدار آن
بور مغناطون است و مقدار آن ![]() است.
است.
مثال 1: بررسی گشتاور مغناطیسی یک الکترون در حالت 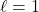
فرض کنید یک الکترون در حالت ![]() قرار دارد. برای این حالت، مقادیر
قرار دارد. برای این حالت، مقادیر ![]() میتواند
میتواند ![]() ،
، ![]() ،
، ![]() باشد. حال برای هر یک از این مقادیر، مقدار
باشد. حال برای هر یک از این مقادیر، مقدار ![]() محاسبه میشود.
محاسبه میشود.
برای ![]() :
:
![]()
برای ![]() :
:
![]()
و برای ![]() :
:
![]()
این مقادیر نشان میدهند که چگونه گشتاور مغناطیسی الکترون در جهتهای مختلف محور ![]() تغییر میکند.
تغییر میکند.
مثال 2: محاسبه مقدار گشتاور زاویهای مداری برای الکترونی در حالت 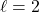
برای یک الکترون با عدد کوانتومی مداری ![]() ، مقدار گشتاور زاویهای مداری به صورت زیر است:
، مقدار گشتاور زاویهای مداری به صورت زیر است:
![]()
این مقدار نشان میدهد که الکترون در این حالت دارای گشتاور زاویهای معینی است.
سوالاتی برای تفکر بیشتر
اگر عدد کوانتومی مداری ![]() برای یک الکترون افزایش یابد، چگونه گشتاور زاویهای مداری آن تغییر میکند؟ آیا میتوانید رابطه بین این دو را توضیح دهید؟
برای یک الکترون افزایش یابد، چگونه گشتاور زاویهای مداری آن تغییر میکند؟ آیا میتوانید رابطه بین این دو را توضیح دهید؟
چگونه میتوان از مفهوم گشتاور دوقطبی مغناطیسی برای فهم بهتر رفتار الکترونها در میدان مغناطیسی استفاده کرد؟
چرا مقادیر گشتاور زاویهای و مغناطیسی الکترون در سیستمهای کوانتومی کوانتیزه است و نمیتواند هر مقداری باشد؟
جمعبندی
گشتاور زاویهای مداری و گشتاور دوقطبی مغناطیسی از مفاهیم پایهای فیزیک کوانتومی هستند که به ما در درک رفتار ذرات زیراتمی مانند الکترونها کمک میکنند. این مفاهیم به ویژه در مطالعه ساختار اتمها و تعاملات آنها با میدانهای مغناطیسی بسیار اهمیت دارند.
