بردار واحد

آشنایی با مفهوم بردار واحد و نوتیشن بردار واحد

در علم فیزیک، یکی از مباحث پایه‌ای که بسیار مهم و کاربردی است، مفهوم بردارها است. بردارها به ما کمک می‌کنند که کمیت‌های برداری مانند نیرو، سرعت، و شتاب را توصیف کنیم. یکی از ابزارهای مهم در کار با بردارها، بردارهای واحد یا همان نوتیشن بردار واحد است. در این مقاله قصد داریم به زبانی ساده، مفهوم بردارهای واحد را توضیح دهیم و نحوه استفاده از آن‌ها را به همراه مثال‌های مختلف بررسی کنیم. این مفاهیم نه تنها برای دانش‌آموزان و دانشجویان مفید است، بلکه برای متخصصین نیز کاربرد دارد.

بردار چیست؟

پیش از آن که به بردارهای واحد بپردازیم، بهتر است ابتدا بردارها را تعریف کنیم. بردار کمیتی است که هم اندازه (بزرگی) و هم جهت دارد. برخلاف کمیت‌های اسکالر که تنها یک عدد دارند، مانند دما یا جرم، بردارها دارای جهت‌گیری در فضا هستند. به عنوان مثال، سرعت یک اتومبیل فقط به اندازه آن (مثلاً 60 کیلومتر بر ساعت) محدود نمی‌شود، بلکه جهت حرکت آن نیز اهمیت دارد (مثلاً به سمت شمال).

تعریف بردار واحد

بردار واحد (Unit Vector) برداری است که بزرگی آن برابر با یک باشد. از آنجا که بردارها می‌توانند در هر جهت باشند، بردارهای واحد می‌توانند در هر جهتی نیز قرار بگیرند، اما همیشه اندازه آنها برابر با یک خواهد بود. بردارهای واحد به ما کمک می‌کنند تا جهت یک بردار را بدون توجه به اندازه آن مشخص کنیم.

نوتیشن بردار واحد: 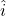$\hat{i}$ , $\hat{j}$ , $\hat{k}$

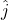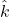
در یک سیستم مختصات سه‌بعدی (محورهای x، y و z)، سه بردار واحد اصلی وجود دارد که برای نشان دادن جهت‌های اصلی در فضای سه‌بعدی استفاده می‌شوند:

بردار واحد $\hat{i}$ : در جهت محور x.
بردار واحد $\hat{j}$ : در جهت محور y.
بردار واحد $\hat{k}$ : در جهت محور z.

این سه بردار واحد در یک سیستم مختصات دست راست تعریف می‌شوند، به این معنی که جهت آنها به گونه‌ای است که با قوانین محصول برداری سازگار است. این بردارها به عنوان ابزارهایی پایه‌ای برای توصیف هر برداری در فضای سه‌بعدی مورد استفاده قرار می‌گیرند.

نوشتن یک بردار به کمک بردارهای واحد

هر بردار در فضای سه‌بعدی را می‌توان به کمک بردارهای واحد $\hat{i}$ ، $\hat{j}$ و $\hat{k}$ نوشت. فرض کنید یک بردار به نام $\vec{a}$ داریم. می‌توانیم این بردار را به صورت زیر بنویسیم:

$\vec{a} = a_x \hat{i} + a_y \hat{j} + a_z \hat{k}$

در این رابطه:

$a_x \hat{i}$ نشان‌دهنده مؤلفه بردار در جهت محور x است.
$a_y \hat{j}$ نشان‌دهنده مؤلفه بردار در جهت محور y است.
$a_z \hat{k}$ نشان‌دهنده مؤلفه بردار در جهت محور z است.

به عبارت دیگر، هر بردار در فضای سه‌بعدی به کمک مؤلفه‌های اسکالر (عدد) $a_x$ ، $a_y$ و $a_z$ و بردارهای واحد $\hat{i}$ ، $\hat{j}$ و $\hat{k}$ توصیف می‌شود.

مثال: تجزیه یک بردار به مؤلفه‌های آن

فرض کنید یک بردار a داریم که اندازه و جهت آن به صورت زیر است:

$\vec{a} = 3 \hat{i} + 4 \hat{j} + 2 \hat{k}$

این به این معناست که بردار a دارای مؤلفه‌ای به اندازه 3 در جهت محور x، مؤلفه‌ای به اندازه 4 در جهت محور y و مؤلفه‌ای به اندازه 2 در جهت محور z است. برای درک بهتر، می‌توانیم این بردار را در فضای سه‌بعدی تجسم کنیم.

بزرگی یک بردار

حال اگر بخواهیم بزرگی یا اندازه این بردار را حساب کنیم، از فرمول زیر استفاده می‌کنیم:

$|\vec{a}| = \sqrt{a_x^2 + a_y^2 + a_z^2}$

در اینجا:

$a_x = 3$
$a_y = 4$
$a_z = 2$

بنابراین:

$|\vec{a}| = \sqrt{3^2 + 4^2 + 2^2} = \sqrt{9 + 16 + 4} = \sqrt{29} \approx 5.39$

بزرگی این بردار تقریباً برابر با 5.39 است.

بردار واحد مرتبط با یک بردار

یکی از کاربردهای مهم بردارهای واحد این است که می‌توانیم از آن‌ها برای محاسبه جهت یک بردار استفاده کنیم. برای یافتن بردار واحدی که جهت یک بردار مشخص را نشان دهد، کافی است بردار اصلی را بر بزرگی آن تقسیم کنیم.

برای مثال، اگر بخواهیم بردار واحد مرتبط با بردار $\vec{a}$ را پیدا کنیم، از فرمول زیر استفاده می‌کنیم:

$\hat{a} = \frac{\vec{a}}{|\vec{a}|}$

در اینجا $\hat{a}$ بردار واحد مرتبط با بردار $\vec{a}$ است. با استفاده از بزرگی‌ای که محاسبه کردیم (5.39)، می‌توانیم بردار واحد را محاسبه کنیم:

$\hat{a} = \frac{1}{5.39} (3 \hat{i} + 4 \hat{j} + 2 \hat{k})$

پس بردار واحد مرتبط با بردار $\vec{a}$ به صورت زیر خواهد بود:

$\hat{a} \approx 0.556 \hat{i} + 0.742 \hat{j} + 0.371 \hat{k}$

کاربردهای بردار واحد در فیزیک

بردارهای واحد در بسیاری از مسائل فیزیکی کاربرد دارند. از جمله کاربردهای مهم آنها می‌توان به موارد زیر اشاره کرد:

نیروها: برای توصیف نیروهایی که در جهت‌های مختلف عمل می‌کنند، می‌توان از بردارهای واحد استفاده کرد.
شتاب: بردارهای واحد در توصیف شتاب اشیاء در سه جهت اصلی فضای سه‌بعدی بسیار مفید هستند.
حرکت چرخشی: در تحلیل حرکت‌های چرخشی و گشتاورها نیز از بردارهای واحد برای نمایش جهت چرخش استفاده می‌شود.

سوالات تفکری برای بررسی بیشتر

برای افزایش درک مفاهیم، سؤالات زیر می‌تواند به خواننده کمک کند تا به تعمق بیشتری بپردازد:

اگر برداری فقط در دو جهت محورهای x و y مؤلفه داشته باشد (یعنی مؤلفه‌ای در جهت z نداشته باشد)، چطور می‌توان بزرگی و جهت آن را محاسبه کرد؟
در چه مواقعی ممکن است بخواهیم از بردار واحد برای نمایش جهت یک بردار استفاده کنیم؟
اگر برداری مؤلفه منفی در یکی از محورهای مختصات داشته باشد، آیا بر بزرگی یا جهت بردار واحد مرتبط با آن تأثیر می‌گذارد؟

جمع‌بندی

در این مقاله، با مفهوم بردار واحد و نوتیشن بردارهای واحد $\hat{\imath}$ , $\hat{\jmath}$ , و $\hat{k}$ آشنا شدیم. این بردارها ابزاری قدرتمند برای تجزیه و تحلیل بردارها در فضای سه‌بعدی هستند. همچنین یاد گرفتیم چگونه یک بردار را به مؤلفه‌های آن تقسیم کرده و بزرگی و بردار واحد مرتبط با آن را محاسبه کنیم. از این دانش در مسائل مختلف فیزیکی مانند نیروها، شتاب‌ها و حرکت‌های چرخشی استفاده می‌شود.