محاسبه میدان الکتریکی به کمک پتانسیل

محاسبه میدان الکتریکی ( $E$ ) از پتانسیل ( $V$ ) در فیزیک

فیزیک الکتریسیته به عنوان یکی از شاخه‌های کلیدی فیزیک، رابطه تنگاتنگی با نیروها و انرژی‌های ناشی از بارهای الکتریکی دارد. یکی از مفاهیم کلیدی در این زمینه، میدان الکتریکی و پتانسیل الکتریکی است. در این مقاله، مفهوم محاسبه میدان الکتریکی ( $E$ ) از پتانسیل الکتریکی ( $V$ ) را با استفاده از قوانین فیزیک بررسی می‌کنیم.

این مقاله، با زبانی ساده و با استفاده از مثال‌های کاربردی، به توضیح این موضوع می‌پردازد. مطالب این مقاله به گونه‌ای طراحی شده است که هم برای دانش‌آموزان و دانشجویان قابل فهم باشد و هم برای افرادی که به طور تخصصی‌تر به فیزیک می‌پردازند، کاربردی باشد.

مفهوم میدان الکتریکی و پتانسیل الکتریکی

پیش از شروع به محاسبات، بیایید ابتدا دو مفهوم مهم میدان الکتریکی و پتانسیل الکتریکی را تعریف کنیم.

میدان الکتریکی (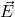 $\vec{E}$ ) چیست؟

میدان الکتریکی یک میدان برداری است که نشان دهنده نیروی وارد شده بر بار الکتریکی در هر نقطه از فضا می باشد. این میدان با علامت $\vec{E}$ نشان داده می شود و واحد آن نیوتن بر کولن ( $N/C$ ) یا ولت بر متر ( $V/m$ ) است. به طور ساده تر، میدان الکتریکی مشخص می کند که اگر یک بار الکتریکی کوچک را در یک نقطه قرار دهیم، چه نیرویی به آن وارد می شود.

پتانسیل الکتریکی (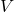 $V$ ) چیست؟

پتانسیل الکتریکی، که با علامت $V$ نشان داده می شود، انرژی پتانسیل الکتریکی به ازای واحد بار است. پتانسیل در یک نقطه مشخص می کند که چقدر انرژی نیاز است تا یک بار مثبت از نقطه مرجع (معمولاً بی نهایت) به آن نقطه انتقال یابد. واحد پتانسیل الکتریکی ولت ( $V$ ) است.

ارتباط بین میدان الکتریکی و پتانسیل الکتریکی

رابطه میان میدان الکتریکی و پتانسیل به این صورت است که میدان الکتریکی برابر است با شیب یا نرخ تغییرات پتانسیل الکتریکی در فضا. در واقع، در هر نقطه، میدان الکتریکی در راستای کاهشی ترین تغییرات پتانسیل قرار دارد. این رابطه با استفاده از مشتقات جزئی قابل بیان است.

فرمول‌های محاسبه میدان الکتریکی از پتانسیل الکتریکی

یکی از مهم‌ترین روابط بین میدان الکتریکی و پتانسیل الکتریکی از طریق مشتق‌گیری از پتانسیل به دست می‌آید. به طور کلی:

$E_s = -\frac{\partial V}{\partial s}$

این معادله به ما می‌گوید که مولفه‌ای از میدان الکتریکی ( $E$ ) در هر جهت خاص ( $s$ ) برابر است با منفی نرخ تغییر پتانسیل ( $V$ ) نسبت به تغییر مکان در آن جهت.

محاسبه مولفه‌های میدان الکتریکی در راستای 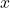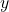$x$ ، $y$ ، و $z$

برای محاسبه میدان الکتریکی در سیستم مختصات دکارتی (سه‌بعدی)، ما می‌توانیم میدان الکتریکی را به مولفه‌های $x$ ، $y$ ، و $z$ تقسیم کنیم:

$E_x = -\frac{\partial V}{\partial x}, \quad E_y = -\frac{\partial V}{\partial y}, \quad E_z = -\frac{\partial V}{\partial z}$

هر کدام از این معادلات نشان‌دهنده نرخ تغییرات پتانسیل الکتریکی در راستای مربوطه هستند.

حالت میدان الکتریکی یکنواخت

در حالت خاصی که میدان الکتریکی یکنواخت باشد (یعنی در همه‌جا یکسان باشد)، معادلات بالا ساده‌تر می‌شوند:

$E = -\frac{\Delta V}{\Delta s}$

در اینجا، $\Delta V$ اختلاف پتانسیل بین دو نقطه و $\Delta s$ فاصله بین آن‌ها است. این معادله برای محاسبات ساده‌تر در مواردی که میدان الکتریکی یکنواخت باشد بسیار کاربردی است.

توضیح اصول و مفاهیم با مثال‌های کاربردی

برای درک بهتر این مفاهیم، بیایید چند مثال کاربردی ارائه دهیم.

مثال ۱: میدان الکتریکی اطراف یک بار نقطه‌ای

فرض کنید یک بار مثبت $Q$ در فضای خالی داریم. پتانسیل الکتریکی در فاصله $r$ از این بار به صورت زیر محاسبه می‌شود:

$V = \frac{kQ}{r}$

که در آن $k$ ثابت کولن و $r$ فاصله از بار است. حالا اگر بخواهیم میدان الکتریکی در فاصله $r$ از این بار را محاسبه کنیم، از فرمول زیر استفاده می‌کنیم:

$E = -\frac{dV}{dr} = -\frac{d}{dr} \left( \frac{kQ}{r} \right)$

با محاسبه مشتق، میدان الکتریکی به صورت زیر به دست می‌آید:

$E = \frac{kQ}{r^2}$

این معادله نشان می‌دهد که میدان الکتریکی با مربع فاصله از بار کاهش می‌یابد.

مثال ۲: میدان الکتریکی یکنواخت بین صفحات موازی

فرض کنید دو صفحه موازی داریم که یکی دارای بار مثبت و دیگری دارای بار منفی است. اختلاف پتانسیل بین این دو صفحه $V$ است و فاصله بین آن‌ها $d$ است. در این حالت، میدان الکتریکی یکنواخت بوده و از رابطه زیر به دست می‌آید:

$E = \frac{V}{d}$

این معادله به ما می‌گوید که میدان الکتریکی یکنواختی که بین دو صفحه موازی وجود دارد، با اختلاف پتانسیل و فاصله بین صفحات مرتبط است.

مثال ۳: توزیع بار در یک رسانای کروی

فرض کنید یک رسانای کروی با شعاع $R$ داریم که به صورت یکنواخت بار $Q$ در سطح آن توزیع شده است. پتانسیل الکتریکی در داخل این کره در هر نقطه‌ای برابر با پتانسیل سطح کره است:

$V = \frac{kQ}{R}$

در این حالت، میدان الکتریکی داخل کره صفر است، اما خارج از کره، میدان الکتریکی مانند یک بار نقطه‌ای عمل کرده و با فاصله $r$ از مرکز کره رابطه دارد:

$E = \frac{kQ}{r^2}$

سؤالاتی برای تفکر و تعامل بیشتر

۱. اگر بار نقطه‌ای منفی بود، چه تغییری در میدان الکتریکی و پتانسیل الکتریکی ایجاد می‌شد؟ ۲. چگونه می‌توان میدان الکتریکی را در یک سیستم پیچیده‌تر با بارهای متعدد محاسبه کرد؟ ۳. در مثال صفحه‌های موازی، اگر فاصله بین صفحات کاهش یابد، چه تأثیری بر میدان الکتریکی دارد؟ ۴. اگر بارها به طور غیر یکنواخت در یک رسانا توزیع شوند، چگونه میدان الکتریکی تغییر می‌کند؟ ۵. آیا میدان‌های الکتریکی می‌توانند همواره یکنواخت باشند؟ در چه شرایطی ممکن است؟

کاربردهای عملی محاسبه میدان الکتریکی از پتانسیل

محاسبه میدان الکتریکی از پتانسیل الکتریکی یکی از اصول کلیدی در طراحی و تحلیل مدارهای الکتریکی، سیستم‌های قدرت، و ابزارهای الکترونیکی است. در علوم مهندسی و فناوری، این محاسبات برای طراحی ترانزیستورها، خازن‌ها، و حتی حسگرهای الکتریکی به کار می‌روند. همچنین، در زمینه‌های علوم محیطی و هواشناسی نیز از این مفاهیم برای مدل‌سازی پدیده‌های طبیعی مانند رعد و برق و توزیع الکتریسیته در جو استفاده می‌شود.

جمع‌بندی

در این مقاله، به بررسی چگونگی محاسبه میدان الکتریکی ( $\vec{E}$ ) از پتانسیل الکتریکی ( $V$ ) پرداختیم و اصول و فرمول‌های مرتبط با این موضوع را مورد بحث قرار دادیم. این مفاهیم به وضوح نشان می‌دهند که میدان الکتریکی مستقیماً با نرخ تغییرات پتانسیل در فضا مرتبط است.

درک دقیق این روابط به ما کمک می‌کند تا بتوانیم مسائل پیچیده‌تری را در حوزه‌های الکترونیک، مهندسی، و فیزیک حل کنیم و همچنین توانایی بهتری در تحلیل و پیش‌بینی رفتار سیستم‌های فیزیکی به دست آوریم.