نوسانات بار و جریان در مدار LC

نوسانات بار و جریان در مدار LC: حفظ انرژی و اصول فیزیکی

نوسانات LC یکی از مفاهیم مهم در فیزیک الکتریسیته و مغناطیس است که بر پایه قانون بقای انرژی قرار دارد. در این مقاله، با زبانی ساده و مثال‌های متنوع، به بررسی این مفهوم، معادلات مربوطه و اصول فیزیکی آن می‌پردازیم. این مقاله به گونه‌ای نگارش شده است که دانش‌آموزان، دانشجویان، علاقه‌مندان به علم فیزیک و حتی افراد متخصص می‌توانند از آن بهره‌مند شوند.

نوسانات LC چیست؟

یک مدار LC از دو عنصر اساسی تشکیل شده است: خازن (C) و سلف (L). در این نوع مدار، بار الکتریکی در خازن ذخیره شده و جریان الکتریکی در سلف جاری می‌شود. این مدار می‌تواند به صورت پایدار نوسان کند و این نوسانات درواقع تبادل انرژی بین خازن و سلف است.

وقتی خازن شارژ شده و سپس تخلیه می‌شود، انرژی الکتریکی به انرژی مغناطیسی در سلف تبدیل می‌شود. سپس این انرژی دوباره به انرژی الکتریکی برمی‌گردد و این چرخه ادامه می‌یابد. این فرآیند تا زمانی که مقاومت در مدار وجود نداشته باشد و اصطکاکی به شکل اتلاف انرژی رخ ندهد، می‌تواند بدون پایان ادامه داشته باشد.

پرسش: اگر مدار LC یک مقاومت جزئی داشته باشد، چه اتفاقی برای نوسانات مدار خواهد افتاد؟ آیا نوسانات همچنان ادامه خواهند داشت؟

معادله دیفرانسیل نوسانات LC

مفهوم نوسانات در مدار LC را می‌توان با استفاده از معادله دیفرانسیل توضیح داد. قانون بقای انرژی بیان می‌کند که انرژی کل در یک مدار LC بدون مقاومت (در حالت ایده‌آل) ثابت می‌ماند. این اصل به معادله دیفرانسیلی زیر منجر می‌شود:

$L \frac{d^2 q}{dt^2} + \frac{1}{C} q = 0$

در این معادله:

$L$ اندوکتانس سلف (بر حسب هنری) است.
$C$ ظرفیت خازن (بر حسب فاراد) است.
$q$ مقدار بار الکتریکی در خازن (بر حسب کولن) است.
این معادله دیفرانسیل رابطه بین بار $q$ و زمان $t$ را توصیف می‌کند و نشان‌دهنده نوسانات بار در مدار است.

پرسش: در معادله فوق، چگونه مقدار بار در طول زمان تغییر می‌کند؟ آیا این تغییرات قابل پیش‌بینی است؟

حل معادله نوسانات LC

با حل این معادله دیفرانسیل، می‌توان به فرمولی برای بار الکتریکی $q$ به عنوان تابعی از زمان $t$ دست یافت. پاسخ این معادله به صورت زیر است:

$q = Q \cos(\omega t + \phi)$

در اینجا:

$Q$ دامنه بار است که نشان‌دهنده حداکثر بار الکتریکی ذخیره شده در خازن است.
$\omega$ بسامد زاویه‌ای نوسانات است که بر اساس اندوکتانس سلف و ظرفیت خازن تعریف می‌شود.
$\phi$ ثابت فاز است که به شرایط اولیه سیستم در زمان $t = 0$ بستگی دارد.

بسامد زاویه‌ای (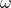 $\omega$ ) چیست؟

بسامد زاویه‌ای $\omega$ به صورت زیر تعریف می‌شود:

$\omega = \frac{1}{\sqrt{LC}}$

این معادله نشان می‌دهد که بسامد نوسانات در یک مدار LC به ظرفیت خازن و اندوکتانس سلف وابسته است. هر چه مقدار $L$ یا $C$ بزرگ‌تر باشد، نوسانات با سرعت کمتری رخ خواهند داد.

پرسش: اگر ظرفیت خازن در مدار افزایش یابد، چه اتفاقی برای بسامد نوسانات خواهد افتاد؟ چرا؟

جریان الکتریکی در مدار LC

در هر لحظه از زمان، علاوه بر بار، جریان الکتریکی نیز در مدار وجود دارد. این جریان به صورت زیر تعریف می‌شود:

$i = -\omega Q \sin(\omega t + \phi)$

در این معادله:

$i$ جریان الکتریکی در مدار است.
$\omega Q$ دامنه جریان، که برابر با $I$ است، نشان‌دهنده حداکثر مقدار جریان در مدار است.
این معادله نشان می‌دهد که جریان در مدار LC به صورت سینوسی تغییر می‌کند و با بار رابطه‌ای معکوس دارد. زمانی که بار در خازن بیشینه است (زمانی که $q = Q$ )، جریان صفر است و زمانی که جریان بیشینه است، بار در خازن صفر است. این موضوع نتیجه مستقیم حفظ انرژی در مدار است.

پرسش: در چه لحظاتی جریان در مدار به بیشینه مقدار خود می‌رسد؟ چه ارتباطی بین بار و جریان وجود دارد؟

اصل بقای انرژی در مدار LC

همان‌طور که اشاره شد، نوسانات در مدار LC نتیجه تبادل انرژی بین خازن و سلف است. در اینجا، انرژی به دو شکل زیر در مدار وجود دارد:

انرژی الکتریکی در خازن:

$U_C = \frac{1}{2} C q^2$

این انرژی زمانی که خازن کاملاً شارژ است، به بیشینه مقدار خود می‌رسد.

انرژی مغناطیسی در سلف:

$U_L = \frac{1}{2} L i^2$

این انرژی زمانی که جریان در سلف بیشینه است، به بیشینه مقدار خود می‌رسد.

در هر لحظه از زمان، مجموع این دو انرژی ثابت باقی می‌ماند که نشان‌دهنده اصل بقای انرژی است:

$U_C + U_L = \text{constant}$

این اصل به ما می‌گوید که انرژی الکتریکی که در خازن ذخیره می‌شود، در طول زمان به انرژی مغناطیسی در سلف تبدیل می‌شود و بالعکس.

پرسش: آیا انرژی می‌تواند از یک مدار LC ایده‌آل از بین برود؟ در صورتی که مقاومت در مدار وجود داشته باشد، چگونه این وضعیت تغییر می‌کند؟

مثال کاربردی: مدار LC ساده

فرض کنید یک مدار LC داریم که خازن آن دارای ظرفیت $C = 1 \mu F$ و سلف آن دارای اندوکتانس $L = 1 mH$ است. می‌خواهیم بدانیم بسامد زاویه‌ای نوسانات در این مدار چقدر است.

راه‌حل:
بسامد زاویه‌ای را می‌توان از فرمول زیر محاسبه کرد:

$\omega = \frac{1}{\sqrt{LC}}$

ابتدا مقادیر $L$ و $C$ را در فرمول جایگذاری می‌کنیم:

$\omega = \frac{1}{\sqrt{(1 \times 10^{-3}) \times (1 \times 10^{-6})}}$

با انجام محاسبات، خواهیم داشت:

$\omega \approx 10^6 \, rad/s$

این به معنای آن است که نوسانات در این مدار با سرعت زاویه‌ای $10^6$ رادیان بر ثانیه رخ می‌دهند.

پرسش: اگر اندوکتانس سلف در مدار دو برابر شود، چه تاثیری بر بسامد زاویه‌ای خواهد داشت؟

کاربردهای نوسانات LC در دنیای واقعی

مدارهای LC در بسیاری از دستگاه‌ها و فناوری‌های مدرن کاربرد دارند. از جمله:

فیلترهای رادیویی: مدارهای LC به عنوان فیلترهایی برای جداسازی سیگنال‌های فرکانس بالا و پایین در رادیوها استفاده می‌شوند.
مدارهای تشدید: این مدارها در دستگاه‌های الکترونیکی برای تنظیم دقیق فرکانس‌ها به کار می‌روند.
تجهیزات مخابراتی: نوسانات LC در تولید و انتقال امواج رادیویی و مخابراتی نقش اساسی دارند.

پرسش: چه تفاوتی بین نوسانات مدار LC و نوسانات مکانیکی (مانند فنر) وجود دارد؟ آیا می‌توان اصول مشابهی در هر دو مشاهده کرد؟

جمع‌بندی

نوسانات LC یکی از مفاهیم اساسی در فیزیک و الکترونیک است که بر پایه قانون بقای انرژی عمل می‌کند. این نوسانات در مدارهایی که از خازن و سلف تشکیل شده‌اند، به عنوان تبادل انرژی بین دو عنصر مدار رخ می‌دهند. معادلات دیفرانسیلی و فرمول‌های مرتبط با این نوع مدارها به ما امکان می‌دهند تا به درک بهتری از رفتار نوسانات و روابط بین بار، جریان و زمان دست یابیم.

به کمک این مفاهیم، می‌توان بسیاری از دستگاه‌ها و سیستم‌های مدرن الکترونیکی را تحلیل و طراحی کرد.