کار انجام شده توسط نیروی متغیر
مفهوم کار انجام شده توسط نیروی متغیر در فیزیک
در علم فیزیک، مفهوم “کار” (Work) یکی از اساسیترین مفاهیمی است که برای درک رفتار نیروها و تأثیر آنها بر اجسام به کار میرود. وقتی نیرویی به جسمی اعمال میشود و آن جسم جابهجا میشود، کار انجام میشود. اما اگر نیروی اعمالشده ثابت نباشد و در طول مسیر تغییر کند، چگونگی محاسبه کار پیچیدهتر میشود. در این مقاله، به بررسی این موضوع با عنوان “کار انجامشده توسط نیروی متغیر” (Work Done by a Variable Force) خواهیم پرداخت.
تعریف کار در فیزیک
در ابتداییترین تعریف، کار را میتوان بهصورت حاصلضرب مقدار نیروی واردشده به جسم در جابهجایی آن جسم تعریف کرد:
![]()
که در آن:
![]() کار انجامشده است،
کار انجامشده است،
![]() نیروی اعمالشده به جسم است،
نیروی اعمالشده به جسم است،
![]() جابهجایی جسم است،
جابهجایی جسم است،
![]() زاویه بین نیروی وارد شده و جهت جابهجایی است.
زاویه بین نیروی وارد شده و جهت جابهجایی است.
این فرمول برای حالتی است که نیروی واردشده ثابت باشد. اما در شرایط واقعی، نیروی اعمالشده به جسم ممکن است بسته به موقعیت جسم تغییر کند. این همان حالتی است که به عنوان “کار توسط نیروی متغیر” شناخته میشود.
کار انجام شده توسط نیروی متغیر
فرض کنید نیرویی که به یک جسم وارد میشود، ثابت نیست و به موقعیت جسم وابسته است. در این حالت، برای محاسبه کار انجامشده توسط نیروی متغیر، نمیتوان از فرمول سادهای که قبلاً معرفی شد استفاده کرد. در عوض، نیاز به انتگرالگیری داریم.
به طور کلی، اگر نیروی وارد بر جسم ![]() باشد و این نیرو به مختصات
باشد و این نیرو به مختصات ![]() وابسته باشد، کار انجامشده در طول جابهجایی از
وابسته باشد، کار انجامشده در طول جابهجایی از ![]() (موقعیت اولیه) تا
(موقعیت اولیه) تا ![]() (موقعیت نهایی) از طریق انتگرال زیر محاسبه میشود:
(موقعیت نهایی) از طریق انتگرال زیر محاسبه میشود:
![]()
این انتگرال نشان میدهد که کار انجامشده توسط نیروی متغیر باید برای هر نقطه از مسیر محاسبه شود و در نهایت با هم جمع شوند.
توضیح اصول کار توسط نیروی متغیر
حالا که فرمول کلی را داریم، اجازه دهید نگاهی دقیقتر به اصول پشت آن بیندازیم. برای درک بهتر، فرض کنید که نیروی ![]() فقط در امتداد محور
فقط در امتداد محور ![]() عمل میکند و وابسته به موقعیت
عمل میکند و وابسته به موقعیت ![]() است. در این حالت، نیرویی که به جسم وارد میشود میتواند در هر نقطه از مسیر تغییر کند و بنابراین کار انجامشده در هر بخش از مسیر متفاوت خواهد بود.
است. در این حالت، نیرویی که به جسم وارد میشود میتواند در هر نقطه از مسیر تغییر کند و بنابراین کار انجامشده در هر بخش از مسیر متفاوت خواهد بود.
مثال ساده از نیروی متغیر
فرض کنید نیرویی به شکل خطی وابسته به موقعیت جسم است، مثلاً:
![]()
که در آن ![]() یک ثابت است. برای محاسبه کار انجامشده در جابهجایی جسم از
یک ثابت است. برای محاسبه کار انجامشده در جابهجایی جسم از ![]() تا
تا ![]() ، باید انتگرال زیر را محاسبه کنیم:
، باید انتگرال زیر را محاسبه کنیم:
![]()
این انتگرال به راحتی حل میشود:
![]()
بنابراین، کار انجامشده توسط نیروی ![]() بهصورت مربعی با فاصلههای شروع و پایان وابسته است.
بهصورت مربعی با فاصلههای شروع و پایان وابسته است.
کار انجام شده در فضاهای سهبعدی
در بسیاری از مواقع، نیروها در سه بعد (محورهای ![]() ،
، ![]() ، و
، و ![]() ) عمل میکنند. اگر نیرو در هر سه بعد تغییر کند، فرمول کار به شکل زیر خواهد بود:
) عمل میکنند. اگر نیرو در هر سه بعد تغییر کند، فرمول کار به شکل زیر خواهد بود:
![]()
در این معادله، نیروها در هر بعد ممکن است بهطور مستقل تغییر کنند و کار انجامشده نیز باید در هر بعد جداگانه محاسبه شود و سپس با هم جمع شود.
مثال از کار در سه بعد
فرض کنید نیرویی داریم که تنها در جهت محور ![]() وابسته به موقعیت است و در دو بعد دیگر ثابت یا صفر است. در این صورت، کار انجامشده در طول جابهجایی از
وابسته به موقعیت است و در دو بعد دیگر ثابت یا صفر است. در این صورت، کار انجامشده در طول جابهجایی از ![]() به
به ![]() فقط به صورت زیر محاسبه میشود:
فقط به صورت زیر محاسبه میشود:
![]()
در این حالت، میتوانیم کار را با همان روشی که در بخش قبلی گفتیم محاسبه کنیم. اما اگر نیرویی در سه جهت مختلف تغییر کند، نیاز به انتگرالگیری در هر سه بعد داریم.
مفهوم نیروهای متغیر در زندگی واقعی
در زندگی روزمره، بسیاری از نیروهایی که بر اجسام وارد میشوند، متغیر هستند. به عنوان مثال:
نیروی فنر: نیرویی که یک فنر به جسم وارد میکند، بسته به میزان فشرده شدن یا کشیده شدن فنر، تغییر میکند. این نوع نیرو به صورت خطی با جابهجایی تغییر میکند (قانون هوک:
![]()
).
نیروی گرانش: نیروی گرانش بین دو جسم به فاصله آنها وابسته است و با افزایش فاصله کاهش مییابد.
نیروی اصطکاک: در برخی موارد، نیروی اصطکاک نیز میتواند به سرعت جسم یا عوامل دیگر وابسته باشد.
تأثیر نیروی متغیر بر انرژی
یکی از کاربردهای مهم محاسبه کار انجامشده توسط نیروی متغیر، تحلیل تغییرات انرژی جسم است. طبق قانون بقای انرژی، کار انجامشده توسط نیرو باعث تغییر در انرژی جنبشی و پتانسیل جسم میشود. به عنوان مثال:
- اگر نیرویی به جسم وارد شود و باعث افزایش سرعت آن شود، کار انجامشده توسط نیرو به افزایش انرژی جنبشی جسم تبدیل میشود.
- اگر نیرویی بر جسم وارد شود و آن را در برابر نیروی گرانش جابهجا کند، این کار میتواند به انرژی پتانسیل جسم اضافه شود.
سوالات تعاملی برای درک بهتر
- آیا میتوانید نمونهای از نیروی متغیر در زندگی روزمره بیاورید؟ چگونه میتوان کار انجامشده توسط این نیرو را محاسبه کرد؟
- اگر نیرویی به صورت غیرخطی با فاصله تغییر کند (مثلاً
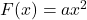 )، چگونه میتوان کار انجامشده توسط این نیرو را محاسبه کرد؟
)، چگونه میتوان کار انجامشده توسط این نیرو را محاسبه کرد؟ - چگونه میتوان از انتگرالگیری برای محاسبه کار در سیستمهای سهبعدی استفاده کرد؟
نتیجهگیری
مفهوم کار انجامشده توسط نیروی متغیر، یکی از مهمترین مفاهیم در فیزیک است که در بسیاری از کاربردهای عملی و نظری استفاده میشود. این مفهوم به ما امکان میدهد تا اثر نیروهایی که در طول مسیر تغییر میکنند را بهدقت محاسبه کنیم. با استفاده از روشهای انتگرالگیری، میتوانیم کار انجامشده توسط این نیروها را در شرایط مختلف جابهجایی و در ابعاد مختلف فضا محاسبه کنیم.
درک این مفهوم میتواند به دانشآموزان و دانشجویان کمک کند تا بهخوبی با رفتار نیروها و تأثیر آنها بر انرژی سیستمها آشنا شوند.
